Лекция 3
3.1. Математические модели и методы в исследовании производственно-экономических ситуаций. Функции, графики, дифференциальное исчисление в экономическом анализе. Исследования и наблюдения в окружающем нас мире показывают, что все экономические величины (цена товара, прибыль субъекта хозяйствования, объем производства, инфляция и безработица и др.) тесно связаны между собой определенным образом. Понятие функции или функциональной зависимости — основное математическое понятие, с помощью которого моделируются взаимосвязи между реальными величинами, качественные и количественные соотношения между технико-экономическими характеристиками и показателями. Функция у = f (х) считается заданной, если известна закономерность, по которой каждому значению х из некоторого множества А соответствует одно вполне определенное значение у из некоторого числового множества В. Любую функцию можно задавать различными способами (наиболее часто используют задание в виде формулы, таблицы или графика, а при использовании ЭВМ — алгоритма). В экономике часто требуется найти наилучшее в том или ином смысле, или оптимальное, значение того или иного показателя: максимальное значение прибыли, производительности оборудования или труда, минимальное значение стоимости, издержек, затрат времени и т.д. Нахождение оптимального значения показателя при этом сводится к нахождению экстремума (максимума или минимума) функции от одной или нескольких переменных. Необходимым условием экстремума функции у = f(x) является равенство нулю ее первой производной. При исследовании на экстремум функций нескольких переменных используются методы дифференциального исчисления, когда решаемые задачи включают не только минимизируемую (максимизируемую) функцию, но и ограничения. К таким задачам относятся задачи математического программирования, для решения которых разработаны специальные методы, опирающиеся на дифференциальное исчисление, и методы теории исчисления операций и предельного анализа. Наряду с этим часто используются понятия средней величины (средние издержки, средний ущерб, средняя прибыль и др.). При этом часто требуется определить, на какую величину улучшится результат, если будут увеличены затраты или, наоборот, насколько уменьшится результат, если затраты сократятся, т. е. необходимо определить предел отношения приростов результатов и затрат с нахождением предельного эффекта. Для решения подобных задач необходимо применение методов дифференциального исчисления — нахождение производной для функции одной переменной и частных производных для функции нескольких переменных (см. Курс Экономической Теории под ред. Сидоровича главы 4 - 30). В экономических приложениях математики широко используются линейные и нелинейные функции двух и более (n) переменных. Упорядоченная пара первых частных производных вида
функции у = f(x 1, x2) двух переменных х 1и х2 обозначается символом grad f (x 1, x2) или и называется градиентом функции [2] от двух переменных х 1и х2 исходной функции f (x 1, x2)или у (x 1, x2). Градиент (см. приложение - 1. Градиент) grad f (x 1, x 2) от функции f(x 1, x 2 ) в точке A(x0 1, x0 2 ) показывает направление самого быстрого роста функции f (x 1, x 2 ) в точке A(x0 1, x0 2 ) (см. рис. 1.1,а). Точка В (x0 1, x0 2) называется критической для функции f(x 1, x2) если координаты x0 1 и x0 2 этой точки удовлетворяют системе уравнений Второй частной производной функции у = f (x 1, x 2 ) двух переменных называется (первая) частная производная от (первой) частной производной. Таким образом, можно получить четыре вторых частных производных:
Если смешанные вторые частные производные
непрерывны, то они обязательно равны. В отличие от смешанных, вторые частные производные Достаточное условие локального экстремума формулируется так. Пусть функция у = f (x 1, x 2 ) имеет критическую точку В(x0 1, x0 2 ), внутреннюю для области определения функции f (x 1, x 2 ) т.е. пусть
1) пусть тогда точка В(x0 1, x0 2 ) - точка локального минимума функции у = f (x 1, x 2 ); 2) пусть тогда точка В(x0 1, x0 2 ) —точка локального максимума функции у = f (x 1, x 2 ); 3) пусть тогда в точке В ( Для функции у = f(x 1, …, x n ) определение условия локального экстремума повторяется почти дословно. В частности, необходимое условие локального экстремума имеет вид:
Достаточное условие локального экстремума из-за сложности записи здесь не приводится. Заметим, что более точными являются термины: безусловный локальный (или глобальный) максимум (минимум); точка безусловного локального (или глобального) максимума (минимума). Иногда вместо термина безусловный используют термин абсолютный. Пример 3.1. Известно, что прибыль (PR) определяется по формуле: PR (х1, х2) = p 0 f (x 1, x 2) – (p 1 x 1+ p 2 x 2) где f (x 1, x 2) - производственная функция фирмы; p 0 — рыночная цена готовой продукции фирмы, р 1и p 2— рыночные цены первого и второго ресурсов (факторов производства). Выражение p 0 f (x 1, x 2 ) — выручка фирмы, a (p 1 x 1+ p 2 x 2) - издержки производства фирмы, если для выпуска продукции ею затрачиваются первый и второй ресурсы в количестве x 1, и x 2 единиц соответственно. Необходимо определить комбинацию В(x0 1, x0 2 ) ресурсов, при которой фирма получит наибольшую прибыль (пример в Excel из лабораторной работы №3 по краскам). Решение. Необходимо найти критические точки функции PR (х1, х2), т. е. найти решение системы уравнений: дPR (х1, х2)/ дх 1, = p 0 д f (x 1, x 2)/ дх 1 – p 1= 0; дPR (х1, х2)/ дх 2, = p 0 д f (x 1, x 2)/ дх 2 – p 2= 0 Из специфики производственной функции (см. лит.[50] гл.10) известно, если ее график напоминает горку, то часто ее критическая точка В (x0 1, x0 2) является единственной и обязательно точкой глобального максимума прибыли у=PR (х1, х2). Графики в экономическом моделировании. Кчислу распространенных зависимостей в экономике можно отнести графики зависимостей спроса и предложения, спроса и дохода, потребления и бюджетного ограничения, издержек и доходов от объема производства. Рассмотрим их более подробно. Функции спроса и предложения p (q) выражают связь цены р
Рис. 3. 1. Распространенные графики функций в экономике: а - градиент функции в задаче потребительского выбора; б - функция спроса в - функция полезностей U (x, у) и бюджетного ограничения; г - функции спроса на товары разного приоритета в зависимости от д - функции издержек C (q), дохода R (q) и прибы-ли П(q) в зависимости от объема производства q. В теории потребительского спроса широко используются xpx + у р у = I где р x р y — цены благ х и у, I — доход потребителя. Чтобы построить графики этих неявно заданных функций,
Как мы знаем, графиком первой функции (кривой безразличия) является гипербола (рис. 3.1,в),а второй Известны также функции Торквинста, моделирующие связь между величиной дохода I и величиной спроса х потребителей
Функции издержек С (q) и дохода R(q) = qp (q) в зависимости от Применение эластичности в математической экономике. Анализ 1) Какие факторы определяют интересующий нас экономический показатель? 2) 3) Какова степень этой зависимости (насколько чувствителен исследуемый экономический показатель кизменению 4) Каково числовое (функциональное) Заметим, анализ чувствительности зависимости функции у = f (х) 1) приростной подход (прирост фактора Δ х → прирост исследуемого показателя Δ у); мера «абсолютной» чувствительности-
2) темповый подход (темп прироста фактора Δ% х → темп при- Δ% y Δ% х → В общем случае эластичностью функции у = f(x) называется Ex (y) = M f где M f — маржинальное (предельное) значение функции у в точке х; А f - среднее значение функции у в точке х. Коэффициент эластичности показывает относительное изменение анализируемого показателя под действием единичного Геометрическая интерпретация эластичности функции проста Е x(у) = ± СВ / СА, где СА - отрезок касательной от точки С(х, у) до ее пересечения с осью х (см. рис. 3.2). Если точки А и В лежат по одну сторону от точки С на каса- В дискретном случае, а также при приближенном определении эластичности по дискретному набору данных вычисление
Рис. 3.2. Графики эластичности в экономическом анализе: а — Еx(у)>1; б — Еx(у)<1; в — Еx(у) отрицательна; г — пределы изменения В зависимости от этого различают: а) конечную (процентную) эластичность
б) среднюю (дуговую) эластичность
в) логарифмическую эластичность
Все эти выражения мало отличаются друг от друга при не- В экономике выделяются следующие виды эластичности: 1. Эластичность спроса по цене (прямая)
Показывает относительное изменение, выраженное в про- 2. Эластичность спроса по доходу I
Характеризует относительное изменение (в процентах) вели- | Ep (q) | < 0, то товары мало - 3. Перекрестная эластичность спроса по цене
Характеризует относительное изменение (в процентах) вели- 4. Ценовая эластичность ресурсов Еpj(Ri) =(дRi/Ri)/(дрi/рj)=(дRi/дрj) (pi / Ri). Характеризует относительное изменение (в процентах) величины спроса на какой-либо ресурс (например, труд) при изменении 5. Эластичность замещения одного ресурса другим ЕRj(Ri) = (dRi / Ri)/(dRj / Rj) =(dRi / dRj) (Rj / Ri). Характеризует необходимые изменения (в процентах) величины одного ресурса (например, капитала) при изменении количества другого ресурса (например, труда) на 1% с тем, чтобы выпуск при этом не изменился. К основным факторам, определяющим эластичность спроса, а) замещаемость блага в потреблении (эластичность спроса б) удельный вес в доходе (эластичность спроса по цене тем в) субъективная необходимость (эластичность спроса по цене тем выше, чем ниже субъективная необходимость в данном благе); r) фактор времени (эластичность спроса по цене обычно Известны следующие теоретические зависимости взаимосвязи эластичности с другими факторами жизни общества: 1. Эластичность выручки от продаж какого-либо товара тесно Еp(R) = Еp(q) + Ер(р) = Ер(q) + 1 = 1 — | Ер(q) |, так как эластичность спроса по цене Ер (q) всегда отрицательна из-за 2. Связь цены и предельных издержек монополиста такова, что величина надбавки киздержкам s обусловливается величиной эластичности. Если совершенно конкурентная фирма устанавливает цену С(П = R — С), имеем: П' — R' — С'= MR — MC = 0,
где П' — знак производной от прибыли. Если вычислить предельную выручку MR и приравнять ее к р = МС/ (1 — 1/ | ЕD |, где ЕD = р / qp '(q), из которого следует, что надбавка кпредельным издержкам в цене должна быть тем меньше, чем выше эластичность спроса (рис.3.2.г). Эта формула позволяет объяснить, как происходит сегментация рынка монопольным производителем с целью дискриминации потребителей и извлечения из этого дополнительной прибыли. Если монополист может устойчиво разделить покупателей MR 1(1 - 1/ | ЕD1 |) =p2 (1 - 1/ | ЕD2 |) = MR2. Отсюда, получаем р1/р2 =(1 - 1 / | ЕD2 |) / (1 - 1 / | ЕD1 |). Следовательно, те покупатели, спрос которых на товар менее 3. Эластичность тесно связана с налоговой политикой и моделями налогов, базирующимися на концепции спроса и предложения. При этом в [50], например, показано, что большее налоговое Аналогичная ситуация возникает, когда налог формально Рассматривая проблему влияния величины налоговой ставки назад
|

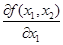 ,
,  или
или 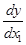 ,
, 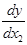
 f (x 1, x2) или grad у (x 1, x2)
f (x 1, x2) или grad у (x 1, x2)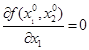 ,
,  . Поэтому точки локального экстремума следует искать только среди критических точек этой функции. Однако критическая точка не обязательно должна являться точкой (локального) экстремума.
. Поэтому точки локального экстремума следует искать только среди критических точек этой функции. Однако критическая точка не обязательно должна являться точкой (локального) экстремума. ;
; 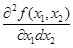 ;
;  ;
; 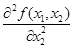 .
. ;
;  принято называть частными.
принято называть частными. ,
,  .
. (или
(или 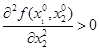 ),
),  ,
,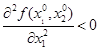 (или
(или  ),
),  ,
, ,
,  ) функция у = f (x 1, x 2 ) локального и, следовательно, глобального экстремума не имеет.
) функция у = f (x 1, x 2 ) локального и, следовательно, глобального экстремума не имеет. ,
,  , …..,
, …..,  .
.
 ,
,  .
.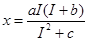 ;
; 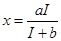 ;
;  ;
;  х.
х.
 =
=  = f '(х)
= f '(х) 
 .
. A f,
A f,
 ;
; ;
; .
. .
. .
. .
.


