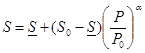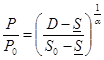Паутинная модель равенства спроса и предложения.

Рассмотрим с позиции потребителя спрос как
функцию от цены D = D(P) и взаимодействие спроса и
предложения.

Пусть известна (получена по эмпирическим данным или иным способом) зависимость
спроса от цены D(P). Предложение также зависит от цены на предлагаемый товар и, вообще говоря, растет с
ростом цены (хотя зависит и от величины прибыли, опре-
деляется не только ценой, но и затратами и, как показано
в лекции 4, может и убывать с ростом цены). Если эта зависимость определяется функцией S(P), то равновесие,
равенство спроса и предложения определяет оптимальную
цену (рис. 3.1), являющуюся корнем уравнения

D(P)=S(P) (5.1)

Можно рассматривать решение этого уравнения как чисто математическую задачу и организовать итерационный процесс (рис. 5.1)

S(Р_k-1) = D(P_k), (5.2)

дающий последовательные приближения Р₀,.P₁,..., Р_k-1, Р_k,....

В главе 4 подробно рассматривался метод простой
итерации. Он является простейшим из класса итерационных
методов.

Итерационные методы — методы построения приближения к решению задачи. Начальное приближение выбирается
из практического смысла задачи, ограничений на область
применимости модели или иных соображений. Для получения
последующих приближений выполняются некоторые действия,
которые называются итерацией или итерацион-ными формула
ми. Полученная последовательность приближений называется
итерационной последовательностью. Теоретически, если ит
ерационный процесс сходится, можно получить сколь угодно близ
кое приближение к решению, неограниченно долго продолжая
итерационный процесс. Например, в п. 4.2 рассматривается
метод простой итерации. Для уравнения х = φ(х) итерация
заключается в построении последовательности точек х⁽⁰⁾,x⁽¹⁾,х⁽²⁾,... — итерационной последовательности, а условие сходимости имеет вид: | φ ' (х)| < 1.

Итерационные методы часто используются при решении
различных задач с помощью вычислительных машин.

В итерационном процессе (5.2) итерационная формула
S(P_k-1) = D(P_k) даёт итерационную последовательность
Р⁽⁰⁾, Р⁽¹⁾, Р⁽²⁾,....

Если итерационный процесс (5.2) сходится (условие сходимости имеет вид: > 1, ниже обсудим, что делать, если процесс расходится), то

либо P₀<Р₂<....< Р^*<...Р₃<P₁,
либо P₀>Р₂>....> Р^*>...Р₃>P₁

и процесс заканчивается и дает значение Р^* с заданной
точностью ε, как только |Р_k — Р_k-1| < ε, и при этом . Заметим, что для фактической реализации этого вычислительного процесса функция D (P)

должна быть такой, чтобы уравнение D(P) = S было
легко разрешимым (лучше всего — аналитически) относительно P. При D = А/P^E это так:

P = (А/S)^1/E, т.е.

(5.2')

Записанный в таком виде итерационный процесс
осуществляется методом простой итерации, блок-схема
метода приведена на рис. 12.2, 12.3.

Из рис. 5.1 видно, что этот процесс графически дает спираль, паутину, наматывающуюся вокруг точки пересечения кривых спроса и предложения и приближающуюся к ней все ближе и ближе, поэтому такой процесс
отыскания равновесной цены получил название паутиной модели. ^[3] Рассмотрим экономическую
интерпретацию
этого процесса,
описывающего
некоторый экономический механизм взаимодействия спроса
и предложения.
Пусть на некоторый товар сложилась цена P₀. Тогда, в соответствии с зависимостью
S(P), предприниматель (или предприниматели) организует производство в объеме S (P_o). Но если при этом
D(P_o) >S(Р₀), то возникает дефицит, и потому данный
объем предложения может быть реализован по более
высокой цене P ₁, для которой S(P₀) = D(Р ₁ ). По цене
Р ₁на следующем отрезке времени организуется произ
водство в объеме S(Р ₁ ), однако при этом возникает пе
репроизводство, цена падает до величины Р ₂, являю
щейся корнем уравнения S(P ₁ ) = D(P ₂ ) и т.д.

Рис. 5.1

Суть итерационного процесса (5.2) в том, что производство реагирует на «вчерашнюю» цену, а спрос —
на «сегодняшнюю» (но «день» равен отрезку времени,
необходимому для организации производства). Подоб­ных примеров колебания производства от дефицита к
перепроизводству и обратно можно наблюдать множество в окружающей нас действитель­ности, но в гибкой, динамической экономике без бурной инфляции этот
про­цесс стабилизации цен идет быстро и довольно гладко, если же гиб­ких рыночных механизмов нет, а инфляция стремительна, он приводит к длительным шараханиям от перепроизводства к дефициту, осложняемым ажиотажным эффектом.

-

Рассмотрим пример:

D(P) =А/Р^E,

S(P) = S + ВР ^α,

где А= D₀P₀^α; Е= 1.5; D₀ = 10; В= (S ₀ – S)/ P₀^α

α=0,5; S =1; S₀=5; Р ₀ =10
D=D ₀

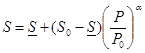
Итерационные вычисления приведены в табл. 5.1.

Таблица 5.1

k		1
P/ P0	1	1,587	1,34	1,45
D		5	6,04	5,73
S	5	6,04	5,73	5,815
k	4	5	6	7
P/ P0	1,435	1,4391	1,4382	1,4383
D	5,815	5,792	5,798	5,797
S	5,192	5,398	5,797	5,797

 

Таким образом, с точностью до 0,001 P ^*/ P ₀ = 1,4383,

P ^* = 14,383 и при этом с той же точностью D = S. Однако,
как отмечено выше, при иных значениях параметров процесс (5.2) может расходиться. Например, если Е = 1, α = 2 (а все остальные данные оставить теми же), то P ₁/ P ₀ = 2 и такому значению P₁ отвечает

S =17>D(P₀) =10, P₂<P₀ и т.д.

С математической точки зрения это означает, что
процесс решения уравнения (5.1) нужно направить в об-
ратную сторону, т.е. вместо (5.2) итерационный процесс
должен иметь вид

S (P_k+1) = D(Р _k ). (5.4)

Сходимость этого процесса для указанных данных
иллюстрирует табл. 5.2. При этом необходима аналитическая разрешимость уравнения S(P) = D, в данном
случае

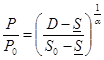
Таблица 5.2

 

k
P/ P0		1,50	1,17	l,36	/,24	I,31
D		6,67	8,40	7,35	7,94	7,59
S			6,67	8,40	7,35	7,94
k
P/ P0	1,284	1,303	1,291		1,294	1,2966
D	7,785	7,676	7,740	7,703	7,725	7,712
S	7,594	7,785	7,676	7, 740	7,703	7,725
k
P/ P0	1,2354	1,2961	1,2957	1,2959	1,2958
D	7,719	7, 715	7,718	7,716	7,717
S	7,712	7,719	7,715	7,718	7,716

 

Экономическая интерпретация процесса (5.4) означает, что предложение должно исходить из данных
прогноза, предприниматель должен ориентироваться не
на «вчерашнюю», а «завтрашнюю» цену. Это не очень
легко реализовать, т.к. информация о цене на предыдущем этапе реальна, доступна фирме, а прогноз нужно
получить и доверие кнему — не абсолютно. Тем не менее, этого можно достичь при наличии аналитических
центров, повышении надежности прогноза и, может
быть, государственным стимулированием в виде дотаций, ссуд, страховок риска. И это необходимо делать.
т.к. при Е/α <; 1 (когда эластичность спроса по цене
меньше эластичности предложения) традиционный про-
цесс (5.2) — расходится.

Нетрудно самостоятельно рассмотреть вопросы,
как изменяется равновесная цена при сдвиге Y= D(P), Y = S(Р) вверх или вниз (при увеличении
или уменьшении спроса или предложения при тех же ценах). Отметим, что к паутинной модели сводится и ряд
других задач: формирование зарплаты, рынок конечных
продуктов, формирование курса валют и т.п.