Градиент.Производной скалярного поля U = U (r) в данной точке r по вектору с, называется предел отношения;
Производной поля U = U (r) в данной точке r в направлении орта с0 называется производная
Градиент поля U (r) (обозначается: grad U или Производная
Координаты градиента: в декартовой системе
в системе цилиндрических координат
в системе сферических координат
В тех точках поля, где линии уровня, проведенные согласно условию на стр. 530, оказываются начерченными более густо, абсолютная величина градиента больше; в точках максимума и минимума поля [в них поверхности (линии) уровня вырождаются в точку] grad U = Q. Дифференциал скалярного поля — полный дифференциал функции U:
назад
|
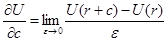
. Производные по вектору с и его орту с0 в данной точке связаны соотношением
в направлении нормали n (n – орт нормали) к поверхности уровня в этой точке (в сторону возрастания функции U): производная по орту в любом другом направлении выражается формулой
U* (
.
равна проекции grad U на направление с0:
