Ранее (в лекции 4) и в лабораторных работах рассматривалась задача одномерной оптимизации — оптимизация прибыли. Прибыль описывалась как функция, зависящая от цены, и находилась цена, при которой прибыль максимальна. Остальные экономические параметры предполагались фиксированными-
. Оптимизировалась функция одного переменного. Однако многие экономические модели сводятся к нахождению экстремумов функции, зависящей от нескольких
переменных, при таких расчётах требуется решать много-
мерную оптимизационную задачу. Рассмотрим задачу
оптимизации функции нескольких переменных.
Пусть экономическая модель описывается набором
параметров (х0, х1,..., хn). Функция и = и (х0, х1,..., х n) (целевая функция) определяет некоторую характеристику, присущую каждому набору. В зависимости от значений функции и выбирается наилучший набор. Пусть наилучший набор (х*0, х*1,..., х*n) характеризуется максимальным значением и.
Рассмотрим строгую формулировку задачи. Пусть
целевая функция и = и (х0, х1,..., хn) определена в неко-
торой области n -мерного пространства. Требуется найти точку х = (x* 0 х* 1 ,..., х* n), в которой значение функции и
максимально:
и = и (х0, х1,..., х n) → тах.
Если в задаче нет ограничений, то максимум
ищется на всей области определения функции и. Чаще
рассматривается задача с ограничением
g 1(x) = 0, g2(x) = 0,..., gm(x) = 0
или, обозначив g = (g1, g2,..., gm)T,
g(x) = 0.
Предположим, ограничений нет. Если целевая
функция непрерывна и дифференцируема как функция
нескольких переменных, то максимум можно искать -
аналогично случаю функции одной переменной:
10 . Выписать необходимое условие максимума
ди/дxi = 0 для i = 0, 1,..., n.
20. Найти стационарные точки функции и, решив
уравнения
ди/дхi = 0, i = 0, 1,..., n.
 30. Перебрать все стационарные значения функции
30. Перебрать все стационарные значения функции
и и найти среди них максимальное или показать, что
решения нет.
Если в задаче
есть ограничение,
то необходимо, что-
бы решение удовлетворяло условиюограничения.
Для геометрической иллюстрации удобнее рассмотреть функцию двух переменны-
х.В случае n переменных рас-смотрение и рас-суждения аналогичны. На рис. 5.2 изображена поверх-
ность, задаваемая целевой функцией двух переменных и
= и(х1, х2). Точка А соответствует максимальному зна-
чению функции при отсутствии ограничений. Проекция
точки А на плоскость (х1,х2) - точка А1 - решение за-
дачи нахождения максимума без ограничений. Пусть
линия сI — Рис. 5.2
график функции g(x)=0, задающей ограничение. Тогда необходимо искать максимальную точку не
на всей поверхности функции и, а только на той её части,
которая удовлетворяет ограничению. Это — линия с. Из
рисунка видно, что точка В соответствует максимально-
му значению функции и при условии g(x) = 0. Проекция
точки В — точка В 1 — решение задачи нахождения мак-
симума при ограничении g(x) = 0.
Рассмотрим один из наиболее эффективных методов решения задачи оптимизации при наличии ограничений типа равенств — метод Лагранжа. Сущность метода состоит в сведении задачи с ограничением к задаче
без ограничений, которую можно решать, используя описанный выше алгоритм.
Пусть функции и (х) = и(х0, х1,..., хn) и g1(х) =
g 1 (x 0, x1,..., хn),..., gm(х) = gm(x0, х1,..., хn) непрерывны и
дифференцируемы. В соответствии с обозначениями
 Требуется найти максимум функции и
Требуется найти максимум функции и
при условии g(x) =0:
и = u(xo, х1,..., хn) → тах, (5.5)
g(xo, х1,..., хn) = 0.
Идея метода Лагранжа состоит в следующем:
из
рис. 5.2 видно, что в точке В1, соответствующей точке В
- решению задачи нахождения максимума при ограни-  чении g(x) = 0 — функция и не имеет максимума. Это
чении g(x) = 0 — функция и не имеет максимума. Это
означает, что частные производные функции и по пере-
менным х0, х1..., хn отличны от 0:
ди/дxi
≠ 0
,
«Подправим» функцию и так, чтобы в точке В1
принималось максимальное значение. Для этого добавим
к ней функции-ограничения, умноженные на неопреде-
лённые множители: зададим числа  (
( =(
=( 1,...,
1,...,  m)) и
m)) и
рассмотрим функцию
L(x,  ) = u(х) —
) = u(х) —  g(х). (5.6)
g(х). (5.6)
Здесь  g(х) — скалярное произведение векторов
g(х) — скалярное произведение векторов 
и g(х):
 g(х) =
g(х) =  1g1(х) +
1g1(х) +  2g2(x)+
2g2(x)+  mgm(х)=
mgm(х)= 
На рис. 5.3 плоскость
(х1, х2) изображена пря-мой g(x), функция L полу-чена по формуле (5.6) и имеет максимум в точке В.
Функция L диффе-ренцируема как разность двух дифференцируемых
функций. Поскольку она достигает максимума в точке
В, то
Рис. 5.3
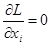 i = 0, 1 ,..., n
i = 0, 1 ,..., n
или по формуле (5.6)
 , i = 0, 1 ,..., n (5.7)
, i = 0, 1 ,..., n (5.7)
Добавив условия ограничения
g(x) = 0 (5.8)
к этим уравнениям, получим систему, из которой определяется решение.
Функция L (x,  ) = L (x0, x1,..., хn,
) = L (x0, x1,..., хn,  1,...,
1,...,  m) называется функцией Лагранжа, переменные
m) называется функцией Лагранжа, переменные  — множителями Лагранжа, а уравнения
— множителями Лагранжа, а уравнения
 , i =0, 1, …, n
, i =0, 1, …, n
— уравнениями Лагранжа.
Сформулируем теорему:
решение задачи (5.5)
удовлетворяет условиям (5.7) и (5.8).
Приведённые выше соображения, разумеется, не являются доказательством. Рассмотрим доказательство этой теоремы:
Пусть задача имеет решение в точке х* и функция ограничений удовлетворяет условию Якоби. Перенумеруем переменные так, чтобы в окрестности точки х разрешить систему ограничений g (x)=0 относительно последних т переменных. Это
можно сделать по теореме о неявной функции. Обозначим эти m
переменных вектором х(2), а оставшиеся (n — т)переменных— х(1). Тогда ограничения можно записать в виде:
Х(2) = h(х(1)).
Здесь h — m-мерный вектор-столбец. Так задача оптимизации (5.5) cвелась к задаче оптимизации функции H(x(1))
при отсутствии ограничений:
H(x(1)) = и (х(1), h(х(1~)) → тах.
Необходимое условие существования максимума функции H(x(1)) имеет вид:
 5.9
5.9
Здесь  — (и — т) -мерная вектор-строка, а
— (и — т) -мерная вектор-строка, а  — матрица размера m*(n — т). Условие g(x) = 0 равносильно условию g(x(1), h(x(1))) = 0. Дифференцируя
— матрица размера m*(n — т). Условие g(x) = 0 равносильно условию g(x(1), h(x(1))) = 0. Дифференцируя
последнее, получим:
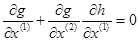 5.10
5.10
Матрица  обратима, т.к. выполнено условие Якоби, и можно разрешить уравнение (5.10):
обратима, т.к. выполнено условие Якоби, и можно разрешить уравнение (5.10):

Подставим эту формулу в уравнение (5.9):

Кроме того,
 (5.11)
(5.11)
Здесь второе слагаемое равно первому, умноженному на
единичную матрицу.
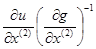 -m-мерная вектор-строка.
-m-мерная вектор-строка.
Обозначим -
её 
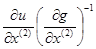 .
.
Тогда уравнения (5.9) и (5.11) можно записать в виде:  .
.
Решение задачи нахождения максимума целевой
функции и при некотором ограничении свелось к задаче нахождения максимума функции Лагранжа L без ограничений.
Рассмотрим алгоритм решения задачи (5.5) нахождения максимума функции нескольких переменных при
наличии ограничения, методом Лагранжа.
1. Вводятся множители Лагранжа λ и определяется функция Лагранжа L(x, λ) = u(х) — λg (х) - и(х0, х1 ,...,х n) - 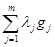 (х0, х1,..., х n).
(х0, х1,..., х n).
2. Выписывается система уравнений (5.8) и (5.7):
 i= 0, 1, …., n
i= 0, 1, …., n
g (x)=0
3. Решается полученная система уравнений. Решения системы  — стационарные
— стационарные
точки функции Лагранжа — при выполнении некоторых
достаточных условий являются решением задачи (5.5).
4. Среди стационарных точек отыскивается решение — точка х =( ), в которой функция и
), в которой функция и
принимает максимальное значение, или доказывается,
что решения нет.
Если ограничение задаётся одной функцией
g1 (х)=0, то рассматривается только один множитель
Лагранжа и функция Лагранжа имеет вид:
L (х,  ) = u(х) —
) = u(х) —  1 g 1(x).
1 g 1(x).
Рассмотрим в этом случае частную производную L по  1
1


т.е. равенство  = 0 – другая форма записи ограничения g 1(х) = 0. -
= 0 – другая форма записи ограничения g 1(х) = 0. -
Поэтому при т = 1уравнения Лагранжа записывают в виде:
 =0, i= 0, 1, …, n;
=0, i= 0, 1, …, n;  = 0 (5.8')
= 0 (5.8')
Рассмотрим пример.
Пусть требуется
вписать прямоугольник
максимальной площади в круг, радиус которого равен r. Введём
систему координат, как
показано на рис. 5.4.
Пусть (х1, х2) — коор-
динаты точки А. Тогда
площадь искомого пря-
моугольника равна
4х1х2, кроме того, точка
А находится на окруж-ности, поэтому должно
выполняться равенство: 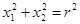 . Из рисунка следую-
. Из рисунка следую-
ет ещё два ограничения: х 1 ≥ 0и х2 ≥ 0, однако они не
являются существенными и их можно пока не рассмат-
ривать. Таким образом, имеется задача нахождения
максимума:
и(х1, х2) =4 х 1 х 2 → тах,
g1(х1, х2) =  = 0.
= 0.
Решим её методом Лагранжа.
Рис.5.4.
Введём множитель Лагранжа λ 1 и составим функцию Лагранжа:
L(x1,x2, λ1) = u(х1,x2) — λ1g1 (х1,x2) = 4 х 1 х 2 — λ1 ( ).
).
Запишем уравнения Лагранжа:
 = 4 х 2 —2 λ1
= 4 х 2 —2 λ1  = 0
= 0
 = 4 х1 — 2 λ1
= 4 х1 — 2 λ1  = 0
= 0
 =
=  = 0
= 0
Решаем полученную систему уравнений:
2 х 2 — λ1  = 0
= 0
2 х1 — λ1  = 0
= 0
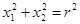
Из первых двух уравнений следует, что  =
=  ,
,
подставив это равенство в третье уравнение, получим
четыре стационарные точки:
 ,
, 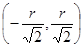 ,
, 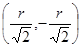 ,
, 
Подставив соответствующие значения переменных в целевую функцию и = 4x1x2, определим максимальное значение. Их два: в точках,  и
и  целевая функция достигает максимума. Проверить это можно непосредственно. Таким образом, точка
целевая функция достигает максимума. Проверить это можно непосредственно. Таким образом, точка 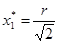 ,
,  - решение задачи нахождения максимума.
- решение задачи нахождения максимума.
Геометрически это означает, что у прямоугольника должны быть равные стороны, т.е. решение — квадрат.
Решение уравнений Лагранжа содержит также и
вектор множителей Лагранжа:  =(
=(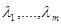 ). С помощью множителей Лагранжа можно получить дополни-
). С помощью множителей Лагранжа можно получить дополни-
тельную информацию о задаче.
Представим ограничения задачи в виде р1(х) = b1 ,
..., рm(х) = bm. Например, функция р i (х) описывает ка-
кой-либо ресурс, а bi — количество этого ресурса. Такие
ограничения легко записываются и в стандартном виде:
g i(х) = рi(х) — bi
Тогда множители Лагранжа, являющиеся решением задачи  показывают чувствительность целевой функции к изменению ресурсов:
показывают чувствительность целевой функции к изменению ресурсов:
 j = 1, …, m.
j = 1, …, m.
Действительно, можно показать, что переменные x0,..., x n, λ 1..., λ m можно считать функциями переменных b 1,..., bm. Тогда функцию Лагранжа также можно рассматривать как функцию переменных b = (bI,..., b m):
L(b) = u(x(b)) — λ (b) (p(x(b)) — b).
Производная функции Лагранжа по b:

В точке, являющейся решением задачи, первые два слагаемых равны 0 в силу уравнений Лагранжа (5.8) и ограничений (5.7), а значение самой функции Лагранжа L равно значению целевой функции и, т.е.
 .
.
Если рассматривается задача оптимизации ресурсов, то целевая функция имеет размерность стоимости (
она описывает, например, прибыль, выручку и т.д.), or-
аничения описывают затраты, поэтому множители Ла-
гранжа имеют размерность цены. Множители Лагранжа
называют также теневыми ценами.

 30. Перебрать все стационарные значения функции
30. Перебрать все стационарные значения функции  Требуется найти максимум функции и
Требуется найти максимум функции и чении g(x) = 0 — функция и не имеет максимума. Это
чении g(x) = 0 — функция и не имеет максимума. Это  (
(
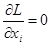 i = 0, 1 ,..., n
i = 0, 1 ,..., n , i = 0, 1 ,..., n (5.7)
, i = 0, 1 ,..., n (5.7) , i =0, 1, …, n
, i =0, 1, …, n 5.9
5.9 — (и — т) -мерная вектор-строка, а
— (и — т) -мерная вектор-строка, а  — матрица размера m*(n — т). Условие g(x) = 0 равносильно условию g(x(1), h(x(1))) = 0. Дифференцируя
— матрица размера m*(n — т). Условие g(x) = 0 равносильно условию g(x(1), h(x(1))) = 0. Дифференцируя 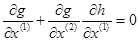 5.10
5.10 обратима, т.к. выполнено условие Якоби, и можно разрешить уравнение (5.10):
обратима, т.к. выполнено условие Якоби, и можно разрешить уравнение (5.10):

 (5.11)
(5.11)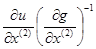 -m-мерная вектор-строка.
-m-мерная вектор-строка.
 .
.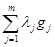 (х0, х1,..., х n).
(х0, х1,..., х n). — стационарные
— стационарные  ), в которой функция и
), в которой функция и 

 = 0 – другая форма записи ограничения g 1(х) = 0. -
= 0 – другая форма записи ограничения g 1(х) = 0. - =0, i= 0, 1, …, n;
=0, i= 0, 1, …, n; 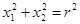 . Из рисунка следую-
. Из рисунка следую- = 0.
= 0. = 0
= 0 = 4 х1 — 2 λ1
= 4 х1 — 2 λ1  = 0
= 0 =
=  =
=  ,
,  ,
, 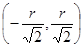 ,
, 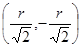 ,
, 
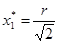 ,
,  - решение задачи нахождения максимума.
- решение задачи нахождения максимума. =(
=(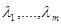 ). С помощью множителей Лагранжа можно получить дополни-
). С помощью множителей Лагранжа можно получить дополни- показывают чувствительность целевой функции к изменению ресурсов:
показывают чувствительность целевой функции к изменению ресурсов: j = 1, …, m.
j = 1, …, m.
 .
.


