Заметки. · Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. · Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются. · Если массив1 и массив2 имеют различное количество точек данных, то функция КОРРЕЛ возвращает значение ошибки #Н/Д. · Если массив1 либо массив2 пуст, или если σ (стандартное отклонение) их значений равно нулю, то функция КОРРЕЛ возвращает значение ошибки #ДЕЛ/0!.
ИНСТРУМЕНТ АНАЛИЗА ДАННЫХ "КОРРЕЛЯЦИЯ";
Определим степень тесноты взаимосвязей между переменными V, Q, P, NCF и NPV (рис.14, практическое занятие №2). При этом в качестве меры будем использовать показатель корреляции R. Выберите в главном меню тему «Сервис» пункт «Анализ данных». Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа. Выберите из списка «Инструменты анализа» пункт «Корреляция» и нажмите кнопку «ОК» (рис.16). Результатом будет появление окна диалога инструмента «Корреляция». Заполните поля диалогового окна, как показано на рис.17 и нажмите кнопку «ОК». Вид полученной ЭТ после выполнения элементарных операций форматирования приведен на рис.18.
Рис. 16 Список инструментов анализа (выбор пункта "Корреляция")
Рис. 17. Заполнение окна диалога инструмента "Корреляция"
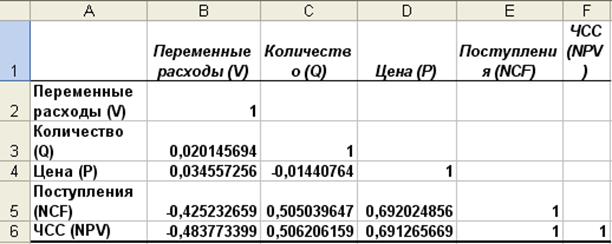
Рис. 18. Результаты корреляционного анализа
Результаты корреляционного анализа представлены в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой. Определите корреляционные характеристики переменных V, Q, P, NCF, NPV практического занятия №1 (рис.4) и сравните с характеристиками переменных практического занятия №2.
Как следует из результатов корреляционного анализа, принятая в процессе решения предыдущего примера гипотеза о независимости распределений ключевых переменных V, Q, P в целом подтвердилась. Значения коэффициентов корреляции между переменными расходами V, количеством Q и ценой Р (ячейки В3:В4, С4) достаточно близки к 0. В свою очередь величина показателя NPV напрямую зависит от величины потока платежей (R = 1). Кроме того, существует корреляционная зависимость средней степени между Q и NPV (R = 0,506), P и NPV (R = 0,69). Как и следовало ожидать, между величинами V и NPV существует умеренная обратная корреляционная зависимость (R = -0,48). Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. В частности в рассматриваемом примере, отсутствие взаимосвязи между переменными затратами V и объемами выпуска продукта Q требует дополнительных объяснений, так как с увеличением последнего, величина V также должна расти (Переменные затраты также часто называют пропорциональными, имея в виду что с увеличением объемов выпуска продукта они растут линейно). Таким образом, установленный диапазон изменений переменных затрат V нуждается в дополнительной проверке и, возможно, корректировке. Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей. При проведении имитационного эксперимента и последующего вероятностного анализа полученных результатов мы исходили из предположения о нормальном распределении исходных и выходных показателей. Вместе с тем, справедливость сделанных допущений, по крайней мере, для выходного показателя NPV, нуждается в проверке. Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова, В простейшем случае для этих целей можно использовать такие характеристики распределения, как асимметрия (скос) и эксцесс. Для нормального распределения эти характеристики должны быть равны 0. На практике близкими к нулевым значениями можно пренебречь. Для вычисления коэффициента асимметрии и эксцесса в ППП EXCEL реализованы специальные статистические функции - СКОС() и ЭКСЦЕСС(). Форматы и краткое описание этих функций приведены ниже:
|



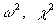 . В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.
. В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.


