Вопрос 18. Моделирование случайных событий и дискретных величин.
Моделирование случайных событий. Простейшими случайными объектами при статистическом моделировании систем являются случайные события. Рассмотрим особенности их моделирования. Пусть имеются случайные числа случайной величины x, равномерно распределенной в интервале (0,1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение
Тогда вероятность события А будет Процедура моделирования в этом случае состоит в выборе значений Таким же образом можно рассмотреть группу событий. Пусть А1, А2,..., Aj — полная группа событий, наступающих с вероятностями р1, р2,..., рs, соответственно. Определим Аm как событие, состоящее в том, что выбранное значение
где
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел Моделирование дискретных случайных величин. Рассмотрим особенности преобразования для случая получения дискретных случайных величин. Дискретная случайная величина hпринимает значения yl≤ y2 ≤... ≤ yj≤... с вероятностями р1,р2,..., рj..., составляющими дифференциальное распределение вероятностей
При этом интегральная функция распределения
Fh(y) = 0; y<y1. (4.19) Для получения дискретных случайных величин можно использовать метод обратной функции. Если x, — равномерно распределенная на интервале (0, 1) случайная величина, то искомая случайная величина hполучается с помощью преобразования
где Алгоритм вычисления по (4.19) и (4.20) сводится к выполнению следующих действий:
если х1<р, то h=у1, иначе если х2<р1+р2, то h=у2 иначе, ………………… (4.21) если ………………… При счете по (4.21) среднее число циклов сравнения
Вопрос 24. Стратегическое планирование машинных экспериментов с моделями систем.
Существует два основных варианта постановки задачи планирования имитационного эксперимента: 1. из всех допустимых выбирается такой план, который позволяет получить наиболее достоверное значение отклика при фиксированном числе опытов. 2. выбирается такой допустимый план, при котором статистическая оценка функции отклика может быть получена с заданной точностью при минимальном объеме испытаний. Решение первой задачи – стратегическое планирование эксперимента. При стратегическом планировании решаются две основные задачи: 1)идентификация факторов; 2)выбор уровня факторов. Под идентификацией факторов понимается их ранжирование по степени влияния на значение наблюдаемой переменной. Факторы обычно разделяются на две группы: - первичные (те факторы, в исследовании влияния которых экспериментатор заинтересован); - вторичные (факторы, которые не являются предметом исследования, но влиянием которых нельзя пренебречь). В процессе идентификации факторов мало влияющие факторы могут не учитываться. Выбор уровней факторов производится с учетом двух противоречивых требований: 1. выбранные факторы должны перекрывать (заполнять) изучаемый диапазон его значений. 2. общее количество уровней по всем факторам не должно приводить к чрезмерному размеру (V) моделирования. Способы построения стратегического плана: Эксперимент, в котором реализуются все возможные сочетания факторов называется ПФЭ (полный факторный эксперимент). Общее число различных комбинаций уровней (точек) в ПФЭ вычисляется по формуле:
где li – число уровней для i-го фактора, k – число факторов. Если число уровней для всех факторов одинаково и равно L, то N=Lk. Недостаток ПФЭ – большие временные затраты на проведение эксперимента, поэтому используются частичные факторные эксперименты (ЧФЭ). Рассмотрим некоторые ЧФЭ: рандомизированный план – предполагает выбор сочетания уравнений для каждого прогона случайным образом. При этом фиксируется число экспериментов, которым экспериментатор считает возможным ограничиться. латинский план («латинский квадрат») используется в том случае, когда проводится эксперимент с одним первичным фактором и несколькими вторичными. эксперимент с изменением факторов по одному. Один из факторов пробегает все свои уровни в то время, как остальные факторы остаются фиксированными. дробный факторный эксперимент. Каждый фактор имеет два уровня (верхний и нижний), поэтому общее число вариантов эксперимента N=2k. Пример латинского плана. Рассматриваются 3 фактора: А,В,С. А – первичный; В,С – вторичные.
План строится таким образом, чтобы в каждой строке и в каждом столбце таблицы данный уровень был представлен только один раз. По данному плану необходимо провести 16 экспериментов. N=16. Для ПФЭ N было бы 43=64. Экономия в 4 раза. Пример дробного факторного эксперимента. k=0
0 – нижний уровень фактора 1 – верхний уровень ЧФЭ N=22=4.
Вопрос 25. Тактическое планирование машинных экспериментов с моделями систем (проблема определения начальных условий и их влияния на достижение установившегося результата, проблема обеспечения точности и достоверности результатов моделирования). Планирование машинных экспериментов – один из этапов имитационного моделирования. План определяет объем и порядок проведения вычислений на ЭВМ, приемы накопления и статистической обработки результатов моделирования системы S Тактическое планирование эксперимента с машинной моделью Тактическое планирование представляет собой определение способа проведения каждой серии испытаний машинной модели Мм, предусмотренных планом эксперимента. Для тактического планирования также имеется аналогия с внутренним проектированием системы S, но опять в качестве объекта рассматривается процесс работы с моделью Ми. Мы системы S связано с вопросами эффективного использования выделенных для эксперимента машинных ресурсов и определением конкретных способов проведения испытаний модели Мы, намеченных планом эксперимента, построенным при стратегическом планировании. Тактическое планирование машинного эксперимента связано прежде всего с решением следующих проблем: 1) определения начальных условий и их влияния на достижение установившегося результата при моделировании; 2) обеспечения точности и достоверности результатов моделирования; 3) уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем; 4) выбора правил автоматической остановки имитационного эксперимента с моделями систем Проблема определения начальных условий и их влияния на достижение установившегося результата при моделировании. Первая проблема при проведении машинного эксперимента возникает вследствие искусственного характера процесса функционирования модели Мм, которая в отличие от реальной системы S работает эпизодически, т. е. только когда экспериментатор запускает машинную модель и проводит наблюдения. Поэтому всякий раз, когда начинается очередной прогон модели процесса функционирования системы S, требуется определенное время для достижения условий равновесия, которые соответствуют условиям функционирования реальной системы. * Таким образом, начальный период работы машинной модели Мм искажается из-за влияния начальных условий запуска модели. Для решения этой проблемы либо исключается из рассмотрения информация о модели Мм, полученная в начальной части периода моделирования (0, Т), либо начальные условия выбираются так, чтобы сократить время достижения установившегося режима. Все эти приемы позволяют только уменьшить, но не свести к нулю время переходного процесса при проведении машинного эксперимента с моделью Мм. * Проблема обеспечения точности и достоверности результатов моделирования. Решение второй проблемы тактического планирования машинного эксперимента связано с оценкой точности и достоверности результатов моделирования (при конкретном методе реализации модели, например, методе статистического моделирования на ЭВМ) при заданном числе реализаций (объеме выборки) или с необходимостью оценки необходимого числа реализаций при заданных точности и достоверности результатов моделирования системы S. Как уже отмечалось, статистическое моделирование системы S — это эксперимент с машинной моделью Мм. Обработка результатов подобного имитационного эксперимента принципиально не может дать точных значений показателя эффективности Е системы S; в лучшем случае можно получить только некоторую оценку Е такого показателя. При этом экономические вопросы затрат людских и машинных ресурсов, обосновывающие целесообразность статистического моделирования вообще, оказываются тесно связанными с вопросами точности и достоверности оценки показателя эффективности Е системы S на ее модели Мм Таким образом, количество реализаций N при статистическом моделировании системы S должно выбираться исходя из двух основных соображений: определения затрат ресурсов на машинный эксперимент с моделью Мм (включая построение модели и ее машинную реализацию) и оценки точности и достоверности результатов эксперимента с моделью системы S (при заданных ограничениях не ресурсы). Очевидно, что требования получения более хороших оценок и сокращения затрат ресурсов являются противоречивыми и при планировании машинных экспериментов на базе статистического моделирования необходимо решить задачу нахождения разумного компромисса между ними. Из-за наличия стохастичности и ограниченности числа реализаций N в общем случае вероятность того, что неравенство
выполняется, называется достоверностью оценки
Величина ε0 = ε/Е называется относительной точностью оценки, а достоверность оценки соответственно будет иметь вид
Для того чтобы при статистическом моделировании системы по заданным Е (или Е0) и Q определить количество реализаций N или, наоборот, при ограниченных ресурсах (известном N) найти необходимые Е и Q, следует детально изучить соотношение (6.7). Сделать это удается не во всех, случаях, так как закон распределения вероятностей величины N = tφ2p(1-p)/(p2ε02) = tφ2(l-р)/(ε02р). (6.10) Соотношение (6.10 – точность результатов моделирования) наглядно иллюстрирует специфику статистического моделирования систем, выражающуюся в том, что для оценивания малых вероятностей р с высокой точностью необходимо очень большое число реализаций N. В практических случаях для оценивания вероятностей порядка 10- k целесообразно количество реализаций выбирать равным 10k+1. Очевидно, что даже для сравнительно простых систем метод статистического моделирования приводит к большим затратам машинного времени.
|

 т. е. возможные значения
т. е. возможные значения (условие 1)
(условие 1) . Противоположное событие
. Противоположное событие  состоит в том, что
состоит в том, что  . Тогда Р(
. Тогда Р(  (условие 2)
(условие 2) . Тогда
. Тогда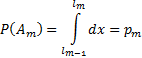
 . Исходом испытания оказывается событие Аm, если выполняется условие 2. Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями р1,p2,…, ps
. Исходом испытания оказывается событие Аm, если выполняется условие 2. Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями р1,p2,…, ps (4.18)
(4.18)
 , (4.20)
, (4.20) — функция, обратная Fh.
— функция, обратная Fh. то h=уm, иначе
то h=уm, иначе













 ≠Е. При этом величина Е называется точностью (абсолютной) оценки:
≠Е. При этом величина Е называется точностью (абсолютной) оценки: (6.6)
(6.6) (6.7)
(6.7) .
. для многих практических случаев исследования систем установить не удается либо в силу ограниченности априорных сведений о системе, либо из-за сложности вероятностных расчетов. Основным путем преодоления подобных трудностей является выдвижение предположений о характере законов распределения случайной величины
для многих практических случаев исследования систем установить не удается либо в силу ограниченности априорных сведений о системе, либо из-за сложности вероятностных расчетов. Основным путем преодоления подобных трудностей является выдвижение предположений о характере законов распределения случайной величины  , т.е. оценки показателя эффективности системы S.
, т.е. оценки показателя эффективности системы S.


