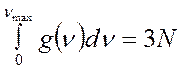Зависимость теплоёмкости от размеров структурных составляющих материалов

Тепловое движение атомов решётки сводится к их колебательному движению около некоторого положения равновесия. Согласно теории Дебая, число типов колебаний кристалла равно числу атомов N, а общее число колебаний трёхмерного тела равно 3N, что соответствует трём степеням свободы на каждое колебание. В соответствии с этим допущением должно выполняться соотношение:

где ν – число колебаний; g(ν) – плотность колебательных состояний; g(ν)dν - число колебаний с частотой от ν+dν; ν_maх – максимальная частота колебаний кристаллической решётки, определяемая из условий равенства полного числа колебаний числу колебательных степеней свободы решётки.

В нанокристаллах могут возникать волны, длина которых не превышает удвоенный размер частицы d. Поэтому со стороны низких частот колебательный спектр наноматериалов, в отличие от крупнокристаллических, ограничен некоторой минимальной частотой ν_min ~ c/2d, где с – скорость света. Таким образом, общее число колебаний для частицы, содержащей N атомов, равно:

Численная величина ν_min зависит от свойств вещества, формы и размеров частицы.

Теоретические исследования показали, что функция распределения частот g(ν) малой частицы прямоугольной формы определяется выражением:

g(ν) = a₁Vν² + a₂Sν + a₃L (1)

где V, S, L – объём, площадь поверхности и общая длина рёбер наночастицы, соответственно; а₁, а₂, а₃ – некоторые коэффициенты.

Согласно теории Дебая теплоёмкость С_v крупнокристаллического твёрдого тела при условии hν < k_BT, соответствует низким значениям абсолютной температуры Т и определяется выражением:

С_v = вVT³ (2)

где V – объём тела; в – некоторый коэффициент.

С учётом уравнения (1) выражение для теплоёмкости наночастицы преобразуется к виду

С_v(r) = в₁VТ³ + в₂SТ² + в₃Т (3)

где в₁, в₂, в₃ – некоторые коэффициенты.

Если принять, что ν_maх в наноматериалах совпадает с максимальной частотой колебаний решётки массивного кристалла, то первый член в уравнении (3) представляет собой дебаевский вклад в теплоёмкость, согласно уравнению (2). В случае наночастиц в выражении для теплоёмкости присутствуют также вклады второго и третьего слагаемых, обусловленные большой поверхностью. Таким образом, из формулы (3) следует, что при hν_mах < k_BT теплоёмкость наночастицы С_v(r) больше теплоёмкости С_v крупнокристаллического материала.

Аналогичные результаты даёт квантовый подход при определении размерной зависимости теплоёмкости.

Интервал температур, в котором колебания решётки следует рассматривать на основе квантовых представлений, весьма узкий. Температура вырождения, при которой в идеальном газе начинают проявляться квантовые эффекты, определяется выражением:

Тв = (h²/mk)(N/V)^2/3

где m – масса; N – число атомов; V – объём системы.

Подстановка числовых значений для протонов даёт значение температуры вырождения порядка 10 К. Таким образом, квантовомеханическое исследование колебаний решётки необходимо при Т < 10 К. При более высоких температурах решётку можно рассматривать с классических позиций.

В квантовом приближении для сферической частицы радиусом r, содержащей N атомов, общее число колебаний равно:

N = (2/9π)r³k_д³ + (1/4π)r²k_д² + (2/3π)rk_д (4)

где k_д – волновой вектор, соответствующий максимальной частоте колебаний ν_maх = k_дс/2π, с – скорость света.

Волновой вектор – вектор, определяющий направление распространения и пространственный период плоской монохроматической волны. Модуль волнового вектора называется волновым числом k. Волновое число определяет пространственный период волны или длину волны λ: k = 2π/λ.

Слагаемые в правой части уравнения (4) учитывают объёмный, поверхностный и линейный вклады, соответственно. С учётом этого уравнения выражение для теплоёмкости кристалла радиуса (r) для области температур hν_min < k_BT приобретает вид:

С_v(r) = С_v + k₁Т²/r + k₂Т/r² (5)

где С_v – теплоёмкость крупнокристаллического материала; k₁, k₂ – некоторые коэффициенты.

При увеличении размера частицы, когда r → ∞, второй и третий члены в уравнении (5) обращаются в нули. Соответственно исчезает разность между теплоёмкостями нано- и крупнокристаллического материала С_v(r) – С_v → 0.

Согласно теоретическим оценкам, в области низких температур при Т → 0 теплоёмкость С_v(r) убывает быстрее, чем теплоёмкость крупнокристаллического материала С_v. Поэтому в области низких температур ∆С = С_v(r) – С_v < 0. Это означает, что существует некоторая температура Т₀, ниже которой ∆С < 0. При Т > Т₀ эта разность становится больше нуля (рис. 1). При высоких температурах теплоёмкость стремится к предельному значению, определённому законом Дюлонга-Пти: С_v → 3R.

Для наночастиц серебра измерения теплоёмкости обнаружили квантовый размерный эффект: при Т < 1 К теплоёмкость наночастиц была