Пример 5.3.3-1.

Два игрока А и В играют в игру, основанную на подбрасывании монеты. Игроки одновременно и независимо друг от друга выбирают герб (Г) или решку (Р) Если результаты двух подбрасываний монеты совпадают (т.е. ГГ или РР), то игрок А получает один доллар от игрока В. Иначе игрок А платит один доллар игроку B.

Следующая матрица платежей игроку А показывает величины минимальных элементов строк и максимальных элементов столбцов, соответствующих стратегиям обоих игроков.

	ВГ	ВР	Минимумы строк
AГ		-1	-1
AР	-1		-1
Максимумы столбцов

Максиминная и минимаксная величины (цены) для этой игры равны -1 доллар и 1 доллар соответственно. Так как эти величины не равны между собой, игра не имеет решения в чистых стратегиях. В частности, если игрок А использует стратегию АГ, игрок В выберет стратегию ВР, чтобы получить от игрока А один доллар. Если это случится, игрок А может перейти к стратегии АР, чтобы изменить исход игры и получить один доллар от игрока В. Постоянное искушение каждого игрока перейти к другой стратегии указывает на то, что решение в виде чистой стратегии неприемлемо. Вместо этого оба игрока должны использовать надлежащую случайную комбинацию своих стратегий. В рассматриваемом примере оптимальное значение цены игры находится где-то между максиминной и минимаксной ценами для этой игры:

максиминняя (нижняя) цена < цена игры < минимаксная (верхняя).

Следовательно, в данном случае цена игры должна лежать в интервале [-1,1], измеряемом в долларах.

[ Таха 11к]

Обозначим p1 вероятность выбора игроком А стратегии АГ. Соответственно, вероятность выбора игроком А стратегии АР будет (1- p1). Тогдасредний платеж игроку А при первой стратегии игрока В равен

,

а при второй стратегии игрока В соответственно

.

поэтому при выборе оптимальной смешанной стратегии

Отсюда .

Подставляя числовые значения, получаем

,

т.е. в оптимальной смешанной стратегии игроку А следует использовать обе стратегии с одинаковой вероятностью. Цена игры в этом простейшем случае будет равна

.

В общем случае следует ожидать, что в игре двух уча­стников с нулевой суммой оба игрока применяют свои оптимальные смешанные стратегии. В частном случае вполне определенной игры оптимальной смешанной стра­тегией будет такая стратегия, в которой чистой стратегии, соответствующей седловой точке, приписана вероятность, равная единице, т. е. векторы оптимальных стратегий единичные. Вообще число ненулевых элементов в векторе оптимальной смешанной стратегии не должно превышать минимальное количество чистых стратегий, имеющихся в распоряжении каждого игрока.

Применяя смешанные стратегии, партнеры ни в одной из партий игры не открывают друг другу своих истинных стратегий. Данная стратегия выбирается с помощью како­го-нибудь механизма случайного выбора (бросание монеты или игральной кости, таблица случайных чисел и т. д.), причем используемые стратегии находятся в соответствии с оптимальными вероятностями. Если бы противнику бы­ло известно, какая именно стратегия будет применена в данной партии, то он мог бы использовать это знание с выгодой для себя. Однако он не может извлечь никакой полезной информации из знания оптимальных вероят­ностей партнера.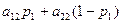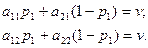