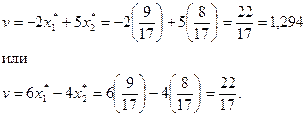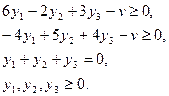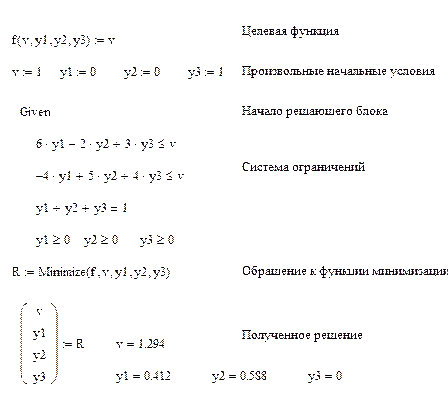Пример 5.4.3-1.
Рассмотрим пример решения матричной игры методом линейного программирования. Вернемся к примеру игры двух участников с нулевой суммой, платежная матрица которой приведена на рис.5.3.1-2:
Эта игра не имеет седловой точки, поэтому решение игры следует искать в смешанных стратегиях. Значение цены игры должно находится между -2 (минимум строк) и 4 (максимум столбцов). Задача линейного программирования для игрока А. Максимизировать z = v при ограничениях
Из системы ограничений можно исключить переменную x2 и перейти к задаче с двумя оптимизируемыми переменными z и v. Максимизировать z = v при ограничениях
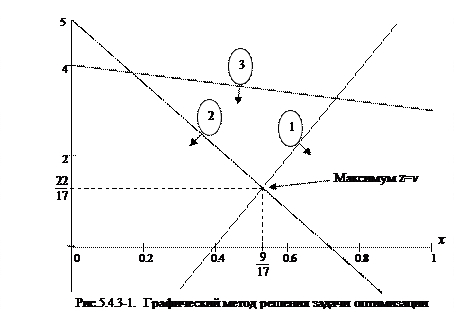
На рис.5.4.3-1 приведен графический способ решения задачи линейного программирования. Цифрами обозначены графики линейных функций, представляющих собой границы областей, в пределах которых выполняются соответствующие ограничения-неравенства. Стрелками показаны направления внутрь областей.
Согласно полученному решению игрок А должен выбирать свою первую стратегию с вероятностью
Задача линейного программирования для игрока А. Максимизировать z = v при ограничениях
Для решения сформулированной задачи линейного программирования воспользуемся системой компьютерной математики Mathcad. Встроенная функция Minimize реализует достаточно универсальный алгоритм оптимизации не требующий вычисления производных. На рис.5.4.3-2 приведено решение поставленной задачи с соответствующим описанием ее постановки.
Оптимальным решением, полученным с помощью программы, является смешанная стратегия y1 = 0,412, y2= 0,588, y3 = 0. Ей соответствует цена игры v = 1,294, т.е. решения полученные игроком А и игроком В дают одинаковую цену игры, что соответствует теореме о минимаксе. Кроме того известно, что в игре 2×n каждый из участников может располагать не более чем двумя активными стратегиями. Равенство нулю вероятности y3 означает, что третья стратегия не является активной и участнику В не следует использовать ее в данной игре. Последний результат подтверждается и графическим решением задачи линейного программирования для игрока А: точка максимума целевой функции не принадлежит прямой (3), соответствующей третей чистой стратегии игрока В.
|

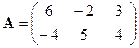 .
.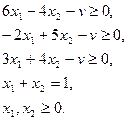
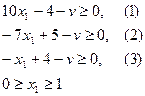
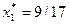 , а вторую – с вероятностью
, а вторую – с вероятностью 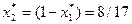 . Цена игры при выборе первым игроком такой смешанной стратегии может быть определена с помощью любого из активных ограничений:
. Цена игры при выборе первым игроком такой смешанной стратегии может быть определена с помощью любого из активных ограничений: