Смешанные стратегии
До сих пор мы не затрагивали вопроса существования ситуаций равновесия в произвольной биматричной игре; между тем, как видно из простейших примеров, ситуаций равновесия может и не быть. Выход из этого положения был найден довольно неожиданный: вводится новый способ выбора стратегий, состоящий в том, что стратегии выбираются не путем их явного указания, а случайным образом, но так, чтобы каждая стратегия имела определенную вероятность быть выбранной. Пусть, например, множество, из которого производится выбор, состоит из трех элементов: X={x1,x2,x3}, при этом вероятность выбора x1 равна 1/2, вероятность выбора x2 равна 1/3 и вероятность выбора x3 равна 1/6. Рассмотрим физический механизм, представляющий собой свободно вращающуюся вокруг неподвижной оси стрелку, а окружность разбита на три дуги x1,x2,x3, длины которых пропорциональны числам 1/2, 1/3, 1/6 (рис.5.3). Если придать стрелке вращение, то вероятность того, что она остановится в секторе x1,x2,x3, равна соответственно 1/2, 1/3, 1/6. Таким образом, данный механизм реализует случайный выбор элементов x1,x2,x3 с вероятностями соответственно 1/2, 1/3, 1/6. Рассмотрим теперь биматричную игру, в которой X={x1,…,xn}– множество стратегий игрока 1, Y={y1,…,ym}– множество стратегий игрока 2, fk – функция выигрыша игрока k=l, 2. Пусть игрок 1 производит выбор своей стратегии случайно, причем вероятность выбора стратегии xi равна Таким образом, допущение случайного выбора игроками своих стратегий означает фактически замену первоначальных множеств стратегий игроков множествами смешанных стратегий. Пусть игрок 1 выбрал смешанную стратегию p=(p1,…,pn), а игрок 2 – смешанную стратегию q=(q1,…,qm). Если игроки производят свой выбор независимо друг от друга, тогда вероятность того, что одновременно игрок 1 выберет стратегию xi, а игрок 2 – стратегию yj,т. е. вероятность ситуации (xi, уj), равна произведению pi×qj, причем в этой ситуации игрок 1 получает выигрыш f1(xi, уj), а игрок 2 – выигрыш f2(xi, уj). В качестве выигрышей игроков при выборе ими смешанных стратегий р и q берутся математические ожидания: для игрока 1
для игрока 2
В итоге мы получаем новую игру, в которой стратегиями игроков являются их смешанные стратегии, М и N – функции выигрыша. Такая игра носит название смешанного расширения первоначальной игры. Одним из основные результатов теории игр является доказанная в 1951 г. американским математиком Дж. Нэшем теорема, согласно которой для всякой биматричной игры существует ситуация равновесия в ее смешанном расширении.
|

 . Тогда можно считать, что он производит выбор (но уже неслучайно!) системы неотрицательных чисел
. Тогда можно считать, что он производит выбор (но уже неслучайно!) системы неотрицательных чисел  .Такая система чисел носит название смешанной стратегии.
.Такая система чисел носит название смешанной стратегии. ,
,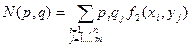 .
.


