Биматричные игры
А. Игры с природой в условиях риска
Для игр с природой в условиях риска характерно то, что вероятности состояний природы известны:
Пусть
Тогда в качестве оптимальной стратегии выбирается та из стратегий
Рассмотрим следующую задачу.
Пример 1. Предприятие готовится к выпуску новых видов продукции. При этом возможны четыре решения
Так как вероятности состояний природы известны, то данная ситуация является задачей принятия решений в условиях риска. Решите задачу, используя критерий оптимизации ожидаемого среднего значения. Определите оптимальную стратегию предприятия.
Б. Игры с природой в условиях неопределенности
Для решения задач данного типа наиболее часто используются критерии Вальда, Сэвиджа и Гурвица.
Критерий Вальда базируется на принципе наибольшей осторожности и использует выбор наилучших из наихудших стратегий. При выборе оптимальной стратегии используется максиминный критерий. Иначе говоря, в качестве оптимальной рекомендуется выбирать ту стратегию, которая гарантирует в наихудших условиях максимальный выигрыш
Критерий Сэвиджа использует матрицу рисков. Критерий Сэвиджа рекомендует выбирать ту стратегию, при которой в наихудших условиях величина риска принимает наименьшее значение:
Критерий Гурвица устанавливает баланс между случаями крайнего пессимизма и крайнего оптимизма путем введения некоторых весовых коэффициентов
Рассмотрим пример, иллюстрирующий применение этих критериев.
Пример 2.
Торговое предприятие планирует продажу сезонных товаров с учетом возможных вариантов поведения покупательского спроса ( Предприятием разработано три стратегии продажи товаров (
Решение Введем данные на рабочий лист в соответствии с Рис. 1 (а, б) Рассмотрим вначале поиск оптимальных стратегий по критериям Вальда и Гурвица.
Критерий Вальда. В диапазон ячеек введите выражение для расчета разности между текущим и максимальным выигрышами. В ячейку G3 введите логическую функцию IF(G3<0;"";"A1") и скопируйте ее (с очевидными изменениями) в необходимый диапазон - это позволит автоматизировать поиск оптимальной стратегии.
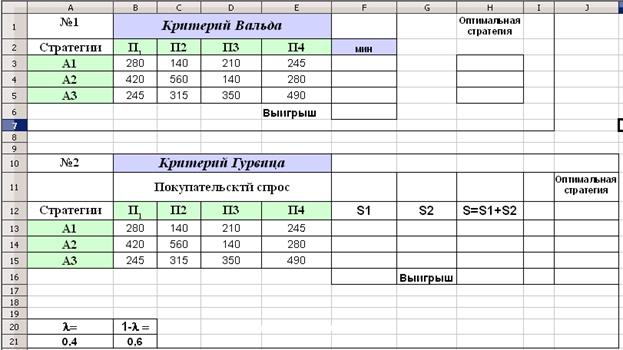
Критерий Гурвица. Обозначим первое слагаемое в выражении (*) через S1, а второе – через S2, введем необходимые формулы для расчета этих составляющих и посчитаем их сумму (столбец H). В ячейках I13:I15 посчитаем разность между текущим и максимальным (ячейка H16) значениями выигрыша, а в диапазон J13:J15 по аналогии с предыдущим случаем введем логические функции IF. При используемом нами значении l=0,4 вы получите определенный результат. Измените значение вероятности, например, возьмите l=0,5. Изменилась ли при этом рекомендуемая стратегия?
Рис. 1 (а). Данные для решения примера 2 (критерии Вальда и Гурвица).
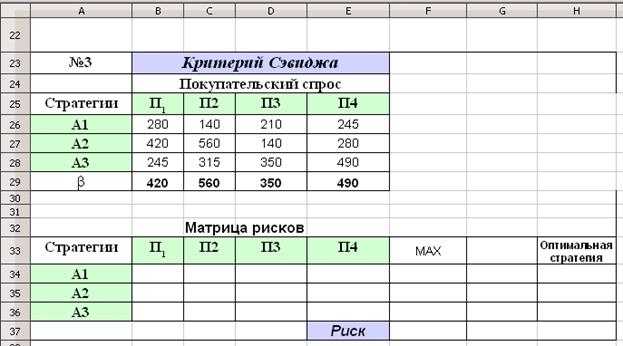
Критерий Сэвиджа. Введите данные в соответствии с Рис. 1 (б). Рассчитайте и разместите в указанном диапазоне ячеек матрицу рисков.
Рис. 1(б). Данные для решения примера 2 (критерий Сэвиджа).
Проведя аналогично предыдущим примерам поиск оптимальной стратегии, сравните полученные при использовании разных критериев результаты.
Биматричные игры Теоретико-игровая модель (короче, игра) является моделью принятия решения в условиях конфликта. Этот конфликт обусловлен тем, что исход определяется совместными действиями нескольких сторон, преследующих различные цели. В теоретико-игровых моделях принято стороны, принимающие решения, называть игроками, а выбираемые ими действия – стратегиями. Если число игроков равно двум и исходы оцениваются численно (каждый игрок дает свою оценку исходу), то получается так называемая биматричная игра; ее удобно задавать таблицей вида табл.6.1, в первый столбец которой выписаны стратегии игрока 1, а в первую строку – стратегии игрока 2. Таблица 6.1. Биматричная игра
Каждый игрок независимо от другого производит выбор своей стратегии. Если игрок 1 выбрал стратегию xi, а игрок 2 – стратегию yj; то получающийся при этом исход оценивается первым игроком числом aij,, а вторым – числом bij; эти числа, называемые соответственно выигрышем игрока 1 и игрока 2, записаны в табл.6.1 на пересечении i-й строки и j-го столбца. Всякую пару стратегий (xi, yj) принято называть ситуацией в игре.
Таблица 6.2. Биматричная игра «два барана»
|
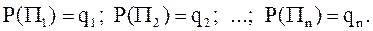
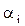- среднее значение (математическое ожидание) выигрыша, которое игрок (ЛПР) стремится максимизировать: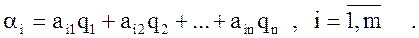
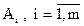, которая соответствует максимальному среднему значению выигрыша (так называемый критерий оптимизации ожидаемого значения):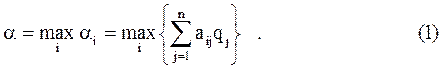
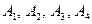, каждому из которых соответствует определенный вид выпуска продукции или их сочетание. Результаты принятых решений существенно зависят от степени обеспеченности производства материальными ресурсами, которая может быть трех видов: П1, П2, П3. Вероятности реализации каждой обстановки равны 
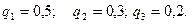Каждому сочетанию решений 
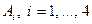и обстановки П j (j = 1,2,3) соответствует определенный выигрыш – эффективность выпуска новых видов продукции. Всевозможные выигрыши представлены платежной матрицей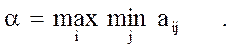
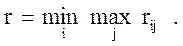
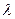и 
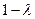, где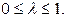 
При этом предполагается, что природа может находиться в самом невыгодном для ЛПР состоянии с вероятностью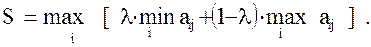 
).
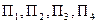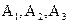). Требуется найти оптимальное поведение торгового предприятия, пользуясь критериями Вальда, Гурвица (при 
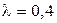) и Сэвиджа, если данные о товарообороте, зависящем от стратегий предприятия и покупательского спроса, могут быть представлены в виде следующей платежной матрицы.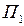
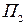
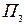
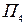
Пример 6-1 (два барана). К нерегулируемому перекрести; едут на высокой скорости под прямым углом друг к другу два автомобиля (рис.5.1). У каждого водителя есть две стратегии: 1) снизить скорость до безопасной (безопасная стратегия) и 2) ехать на высокой скорости (рискованная стратегия).
