Оптимальность в форме равновесия
Проанализируем ситуации этой игры с точки зрения их устойчивости. Ситуация (Б, Б) является неустойчивой, так как в этой так как в этой ситуации игрок 1 может получить лучший для себя исход, изменив стратегию Б на стратегию Р. В этом случае он получит выигрыш 3 вместо 1. То же самое справедливо в ситуации (Б, Б) и для игрока 2. Точно так же неустойчивой является и ситуация (Р, Р). Итак, неустойчивость какой-либо ситуации проявляется в том, что в случае ее возникновения ей грозит распад, который обусловлен возможностями одного из игроков получить лучший для себя исход путем одностороннего изменения своей стратегии. Ситуации (Б, Р) и (Р, Б), напротив, обе являются устойчивыми: если они возникли, то ни у одного из игроков нет оснований отходить от них, односторонне изменив свою стратегию. Устойчивость, например, ситуации (Б, Р) проявляется в том, что каждый из водителей, узнав о стратегии другого, будет придерживаться выбранной им стратегии: первый будет продолжать ехать на низкой скорости, а второй – на высокой. Описанные в примере устойчивые ситуации называются в теории игр ситуациями равновесия (или равновесными в смысле Нэша — по имени американского математика Джона Нэша). В общем случае для биматричной игры, заданной в виде табл.6.1, равновесность ситуации Равновесные ситуации можно рассматривать как оптимальные совместные решения, причем оптимальность равновесной ситуации проявляется в отношении ее устойчивости. Возникает, однако, вопрос: а насколько хороши равновесные ситуации в других отношениях, прежде всего в отношении выигрышей игроков? Ведь каждый игрок может рассматривать выбор своей стратегии как принятие решения в условиях неопределенности (при этом другой игрок выступает в качестве среды) и может выбрать, например, свою максиминную стратегию, гарантирующую ему независимо от действий другого игрока максимин. Не получит ли он в таком случае больший выигрыш, чем в ситуации равновесия? Оказывается, что нет, и в этом очень легко убедиться. Действительно, пусть
откуда, используя определение ситуации равновесия, получаем
Аналогично получаем
Таким образом, в ситуации равновесия каждый из игроков имеет выигрыш, не меньший, чем «свой» максимин. Казалось бы, что все в порядке, но тут нас подстерегает довольно серьезная неприятность, состоящая в том, что компоненты ситуаций равновесия могут не составить снова ситуации равновесия. Вначале это утверждение кажется парадоксальным: если В рассмотренном выше примере «два барана» было две ситуации равновесия (Р, Б) и (Б, Р); взяв от первой ситуации первую компоненту, а от второй — вторую, получим неравновесную ситуацию (Р, Р), приводящую к тому же к наихудшему для обоих игроков исходу (именно так поступили два барана, хотя неизвестно, руководствовались ли они концепцией равновесия). Указанное выше обстоятельство можно пояснить геометрически следующим образом. Представим стратегии игрока 1 точками горизонтального отрезка, а стратегии игрока 2 – точками вертикального отрезка (см. рис.5.2), тогда все ситуации представляются точками прямоугольника. Множество всех ситуаций равновесия игры образует некоторую область D внутри этого прямоугольника (которая может быть и пустой). Очевидно, что требование, чтобы всякая ситуация, составленная из компонент ситуаций равновесия, снова была ситуацией равновесия, означает с геометрической точки зрения, что область D имеет вид прямоугольника (рис. 5.2.б); такое множество ситуаций равновесия называется поэтому прямоугольным (заметим, что множество, состоящее из единственной ситуации равновесия, является прямоугольным). Если же множество ситуаций равновесия не является прямоугольным, то выбор игроком 1 стратегии, являющейся первой компонентой некоторой ситуации равновесия, не гарантирует образования равновесной ситуации, даже если игрок 2 также выберет стратегию, являющуюся второй компонентой некоторой ситуации равновесия (рис.5.2,а). Так как в общем случае множество ситуаций равновесия биматричной игры не является прямоугольным, то можно сделать вывод, что оптимальность в форме равновесия относится именно к ситуациям, а не к их компонентам – стратегиям игроков.

|

 означает, что для всех i=1,…n; j=1,…,m
означает, что для всех i=1,…n; j=1,…,m 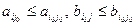 .
.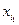 – максиминная стратегия игрока 1. Тогда
– максиминная стратегия игрока 1. Тогда
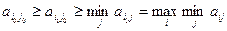 .
. .
. ; составляя их, получаем ту же ситуацию
; составляя их, получаем ту же ситуацию 


