Теорема о минимаксе
Основной теоремой в теории игр с нулевой суммой является теорема о минимаксе, согласно которой любая конечная игра имеет решение, если допускается использование смешанных стратегий. Обозначим через
матрицу-столбец, состоящую из вероятностей xi, выбора i-й стратегии игрока А, и через
соответственно матрицу-столбец (вектор) вероятностей появления стратегий игрока B. В приведенных формулах
Теперь можно ставить вопрос об оптимальном выборе стратегии. В этом случае векторы х и у называются смешанными стратегиями игроков А и В соответственно. Если в векторе х или у (или обоих вместе) все составляющие равны нулю, за исключением одной, то такую стратегию называют чистой. Чистая стратегия может быть оптимальной только при наличии седловой точки. В противном случае следует говорить об оптимальных смешанных стратегиях. При наличии смешанных стратегий следует оперировать не платежами, а средним значением (математическим ожиданием) платежей. Допустим, что игрок А выбирает чистую стратегию i, а игрок В – смешанную стратегию у. Тогда средний платеж игроку А равен:
Величина ui представляет собой i-ю составляющую вектора-столбца u:
Если игрок В применяет чистую стратегию j, а игрок А – смешанную стратегию х, то средний платеж игроку А равен:
Величина lj представляет собой j-ю составляющую матрицы-строки lt:
Если игроки А и В применяют смешанные стратегии х и у соответственно, то средний платеж игроку А
Основная теорема теории игр, теорема о минимаксе, утверждает, что максимин среднего платежа равен минимаксу среднего платежа, т.е.
Из этого равенства следует, что существует такая пара стратегий
для всех x и y. В этом случае пара векторов (х*, у*) называется решением игры, оптимальными стратегиями, a v – ценой игры, т. е. всегда существует решение игры в классе чистых или смешанных стратегий. В оптимальную смешанную стратегию не обязательно входят все чистые стратегии. Поэтому для тех чистых стратегий, которые входят в оптимальную смешанную стратегию, вводят специальный термин – активные стратегии. С активными стратегиями связано очень важное положение. Оказывается, что оптимальная смешанная стратегия, примененная против любой активной стратегии, дает цену игры. И, наоборот, любая активная стратегия, примененная против оптимальной смешанной стратегии, также дает цену игры. Это значит, что если один из игроков применяет оптимальную смешанную стратегию, то выигрыш (платеж) остается неизменным и равным цене игры v, независимо от стратегии другого игрока, если тот применяет одну из своих активных стратегий, их оптимальную и неоптимальную комбинацию (т. е. не выходит из класса активных стратегий). Это очень важное положение широко используется при определении решений игр. При этом необходимо прежде всего определить активные стратегии свои и противника. Далее, приравняв средние платежи при активных стратегиях противника и смешанных из активных своих стратегий цене игры, получим систему алгебраических уравнений, решив которые, можно найти свою оптимальную смешанную стратегию.
|




 .
. .
.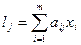
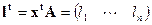 .
. .
. .
. , что
, что



