Биматричная игра называется почти антагонистической, если при переходе от одной ситуации к другой увеличение выигрыша одного из игроков сопровождается уменьшением выигрыша другого:
 .
.
Множество ситуаций равновесия почти антагонистической игры обладает следующим важным свойством: во-первых, оно является прямоугольным и, во-вторых, для каждого из игроков его выигрыш в любой ситуации равновесия один и тот же.
Действительно, пусть  и
и  – две ситуации равновесия почти антагонистической игры. Рассмотрим часть таблицы игры, образованную строками i1,i2 и столбцами j1, j2 (табл.6.4). Так как
– две ситуации равновесия почти антагонистической игры. Рассмотрим часть таблицы игры, образованную строками i1,i2 и столбцами j1, j2 (табл.6.4). Так как  – ситуация равновесия, то
– ситуация равновесия, то  , а значит, по условию почти антагонистичности
, а значит, по условию почти антагонистичности 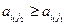 . Далее, так как
. Далее, так как  – ситуация равновесия, то
– ситуация равновесия, то  . Получаем
. Получаем  , откуда
, откуда  . Но ввиду равноправия ситуаций
. Но ввиду равноправия ситуаций  и
и  выполняется и обратное неравенство
выполняется и обратное неравенство  поэтому
поэтому  . Аналогично
. Аналогично  Получаем, что
Получаем, что  ситуация равновесия, причем выигрыши игроков в этой ситуации те же, что и в ситуации равновесия
ситуация равновесия, причем выигрыши игроков в этой ситуации те же, что и в ситуации равновесия  . Таким образом, сформулированное выше свойство ситуаций равновесия почти антагонистической игры доказано.
. Таким образом, сформулированное выше свойство ситуаций равновесия почти антагонистической игры доказано.
Таблица 6.4. Матрица почти антагонистической игры
Предположим теперь, что игрок 1 использует стратегию  , являющуюся первой компонентой ситуации равновесия. Тогда для любого j=l,...,m выполняется
, являющуюся первой компонентой ситуации равновесия. Тогда для любого j=l,...,m выполняется  и по определению почти антагонистической игры
и по определению почти антагонистической игры  Но, как мы знаем, выигрыш игрока в ситуации равновесия не меньше, чем его максимин, поэтому, обозначая
Но, как мы знаем, выигрыш игрока в ситуации равновесия не меньше, чем его максимин, поэтому, обозначая 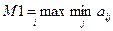 , получаем
, получаем  .
.
Полученное неравенство означает, что в почти антагонистической игре применение игроком стратегии, являющейся компонентой ситуации равновесия, гарантирует ему по крайней мере его максимин.

 .
. и
и  – две ситуации равновесия почти антагонистической игры. Рассмотрим часть таблицы игры, образованную строками i1,i2 и столбцами j1, j2 (табл.6.4). Так как
– две ситуации равновесия почти антагонистической игры. Рассмотрим часть таблицы игры, образованную строками i1,i2 и столбцами j1, j2 (табл.6.4). Так как  , а значит, по условию почти антагонистичности
, а значит, по условию почти антагонистичности 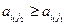 . Далее, так как
. Далее, так как  . Получаем
. Получаем  , откуда
, откуда  . Но ввиду равноправия ситуаций
. Но ввиду равноправия ситуаций  поэтому
поэтому  . Аналогично
. Аналогично  Получаем, что
Получаем, что  ситуация равновесия, причем выигрыши игроков в этой ситуации те же, что и в ситуации равновесия
ситуация равновесия, причем выигрыши игроков в этой ситуации те же, что и в ситуации равновесия 







 и по определению почти антагонистической игры
и по определению почти антагонистической игры  Но, как мы знаем, выигрыш игрока в ситуации равновесия не меньше, чем его максимин, поэтому, обозначая
Но, как мы знаем, выигрыш игрока в ситуации равновесия не меньше, чем его максимин, поэтому, обозначая 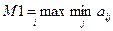 , получаем
, получаем  .
.


