Оптимальное решение игры двух лиц с нулевой суммой

Поскольку игры берут свое начало в конфликте интересов, оптимальным решением игры является одна или несколько таких стратегий для каждого из игроков, при которых любое отклонение от выбранных стратегий не улучшает плату тому или другому игроку. { Односторонне отклонение от выбранных стратегий не улучшает плату отошедшему от оптимальной стратегии игроку}

В качестве основного допущения в теории игр двух лиц с нулевой суммой принимается, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях противника. Однако наибольший гарантированный выигрыш определяется при том условии, что избранная данным игроком стратегия становится изве­стной противнику, который затем выбирает свою опти­мальную стратегию. Пусть игрок А считает, что, какую бы строку он ни выбрал, игрок В выберет столбец, максимизи­рующий его выигрыш и тем самым минимизирующий выигрыш игрока А. Тогда можно исключить из платежной матрицы все элементы, оставив в каждой строке только по одному элементу, соответствующему минимальному платежу. Оптимальная стратегия игрока А, которая обес­печит ему наибольший из возможных выигрышей вне зави­симости от стратегии противника, будет состоять в выборе строки с самым высоким из таких минимальных платежей. Таким образом, игрок А выбирает i-ю стратегию, которая является решением задачи

.

Стратегия, соответствующая максимальному значению минимумов строк, является максиминной стратегией.

Игрок В точно так же стремится обеспечить себе наивыс­шую величину выигрыша (т. е. наименьшее значение пла­тежа своему противнику) вне зависимости от стратегии, избираемой партнером. Следовательно, игрок В может исключить из платежной матрицы все элементы, оставив в столбце только по одному элементу, соответствующему максимальному платежу. Его оптимальной стратегией будет столбец с наименьшим значением максимального платежа. Таким образом, игрок В выбирает j-ю стратегию, которая является решением задачи

.

Стратегия, соответствующая минимальному значению мак­симумов столбцов, называется минимаксной стратегией.

Если игрок A придерживается максиминной стратегии, то его выигрыш будет не меньше максиминного значения, т.е.

.

Если игрок B избирает минимаксную стратегию, то его проигрыш будет не больше минимаксного значения, т.е.

Если

,

то игроки получают свои гарантированные платежи. В этом случае их стратегии оказываются совместимыми, а платеж­ная матрица имеет седловую точку на пересечении i-й стро­ки и j-го столбца, т. е. элемент 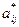является одновременно минимальным в своей строке и максимальным в своем столбце. Седловая точка матрицы является ценой игры. Седловая точка соответствует положению равновесия, если один из игроков использует стратегию, соответствующую седловой точке, то другому выгоднее всего избрать свою стратегию, также отвечающую седловой точке. Игра двух участников с нулевой суммой, имеющая седловую точку, называется вполне определенной. Разумно ожидать, что в игре такого типа оба партнера изберут стратегию седловой точки.