 гл XVIII; [3] № 372, 382, 397, 405, 418, 421;
гл XVIII; [3] № 372, 382, 397, 405, 418, 421;
[1] гл. XIX § 1-4; [3] № 452, 455, 457, 496.
Разберите решениезадачи 4 данного пособия.
Задача 4. Даны координаты трех точек:
А (3; 0; —5), В(6, 2,1), С(12,-12,3).
Требуется: 1) записать векторы 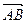 и
и 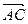 в системе орт и найти модули этих векторов; 2) найти угол между векторами
в системе орт и найти модули этих векторов; 2) найти угол между векторами 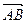 и
и 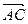 ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору
; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору 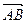 .
.
Решение. 1. Если даны точки 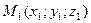 и
и  , то вектор
, то вектор  через орты
через орты 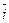 ,
, 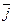 ,
, 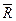 выражается следующим образом:
выражается следующим образом:  =
= 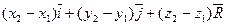 = а
= а  . (1)
. (1)
Подставляя в эту формулу координаты точек А и В, имеем:
 .
.
Подобным образом 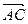 = (12-3)
= (12-3) 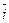 +(-12-0)
+(-12-0) 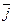 +|(3+5)
+|(3+5) 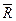 = 9
= 9 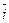 -12
-12 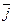 +8
+8 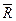 .
.
Модуль вектора  вычисляется по формуле
вычисляется по формуле
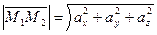 . (2)
. (2)
Подставляя в формулу (2) найденные ранее координаты векторов  и
и 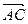 , находим их модули:
, находим их модули:
 ,
, 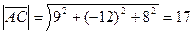 .
.
- Косинус угла
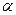 , образованного векторами
, образованного векторами 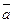 и
и  , равен их скалярному произведению, деленному на произведение их модулей
, равен их скалярному произведению, деленному на произведение их модулей
cоs 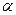 =
= 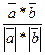 . (3)
. (3)
Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных произведений одноименных координат, то 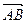 *
* 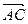 =3*9+2*(-12)+6*8=51. Применяя (3), имеем:
=3*9+2*(-12)+6*8=51. Применяя (3), имеем:
cоs 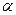 = соs (
= соs (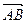 ^
^ 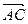 )=
)=  ;
; 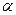
 64
64 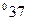 '.
'.
- Известно, что уравнение плоскости, проходящей через точку М0(
 ) перпендикулярно вектору
) перпендикулярно вектору 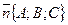 , имеет вид
, имеет вид
А (х-хо) +В (у-у0) + С(г-z0) =0. (4)
По условию задачи искомая плоскость проходит через точку С(12; —12; 3) перпендикулярно вектору 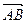 {3; 2; 6}. Подставляя в (4) А=3, В=2, С=6, х0=12, у0=—12, z0 = 3, получим:
{3; 2; 6}. Подставляя в (4) А=3, В=2, С=6, х0=12, у0=—12, z0 = 3, получим:
3(х-12) +2(у+12)+6(z-3)=0,
3х+2у+6z-30=0 — искомое уравнение плоскости.
Вопросы для самопроверки
- Какие величины называются скалярными? векторными?
- Какие векторы называются коллинеарными?
- Какие два вектора называются равными?
- Как сложить два вектора? Как их вычесть?
- Как найти координаты вектора по координатам точек его начала и конца?
- Назовите правила сложения, вычитания векторов, заданных в координатной форме. Как умножить вектор на скаляр?
- Дайте определение скалярного произведения двух векторов. Перечислите основные свойства скалярного произведения.
- Как найти скалярное произведение двух векторов по их координатам?
- Напишите формулу для определения угла между двумя векторами.
- Напишите условия: коллинеарности двух векторов; их перпендикулярности.
- Напишите общее уравнение плоскости.
- Напишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
- Какой вид имеет уравнение плоскости, проходящей через три данные точки?
- Напишите формулу для определения расстояния от точки до плоскости.

 гл XVIII; [3] № 372, 382, 397, 405, 418, 421;
гл XVIII; [3] № 372, 382, 397, 405, 418, 421;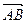 и
и 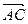 в системе орт и найти модули этих векторов; 2) найти угол между векторами
в системе орт и найти модули этих векторов; 2) найти угол между векторами 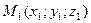 и
и  , то вектор
, то вектор  через орты
через орты 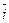 ,
, 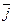 ,
, 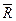 выражается следующим образом:
выражается следующим образом: 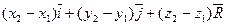 = а
= а  . (1)
. (1) .
.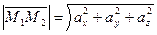 . (2)
. (2) и
и  ,
, 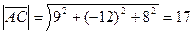 .
.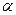 , образованного векторами
, образованного векторами 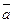 и
и  , равен их скалярному произведению, деленному на произведение их модулей
, равен их скалярному произведению, деленному на произведение их модулей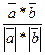 . (3)
. (3) ;
;  64
64 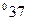 '.
'. ) перпендикулярно вектору
) перпендикулярно вектору 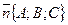 , имеет вид
, имеет вид


