Тема II. РЯДЫ
Разберите решение задач 14, 15 данного пособия. Задача 14. Написать первые три члена ряда найти интервал сходимости ряда и исследовать его сходимость на концах интервала. Решение. Беря последовательно m=1, 2, 3,..., запишем данный ряд в виде:
Для нахождения области сходимости ряда применим признак Даламбера
Данный ряд сходится абсолютно при тех значениях х, которые удовлетворяют неравенству
Исследуем сходимость ряда на концах полученного интервала. При х=- Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при m х=- При х= Исследуем сходимость этого ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл
Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при х=
Таким образом, -
Задача 15. Вычислить Решение. Представим подынтегральную функцию в виде степенного ряда. Заменив х в разложении функции sinх на sin Тогда
=3-
Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвертым его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда
Вопросы для самопроверки 1. Что называется числовым рядом? 2. Что называется n-й частичной суммой числового ряда? 3. Какой числовой ряд называется сходящимся? 4. Что является необходимым условием сходимости числового ряда? 5. Назовите достаточные признаки сходимости, основанные на сравнении рядов. 6. Назовите признак Даламбера сходимости рядов. 7. В чем состоит интегральный признак сходимости Коши? 8. Какие ряды называются знакочередующимися? Приведите примеры. 9. Сформулируйте признак Лейбница сходимости знакочередующихся рядов. 10. Какие знакочередующиеся ряды называются абсолютно сходящимися? условно сходящимися? 11. Дайте определение степенного ряда и области его сходимости. 12. Как найти область сходимости степенного ряда? 13. Запишите разложение в степенной ряд функций In (1+х).
|

 гл. XX1 § 1 — 14:
гл. XX1 § 1 — 14:  № 2424, 2426, 2474, 2475, 2503, 2519. 2533.
№ 2424, 2426, 2474, 2475, 2503, 2519. 2533.
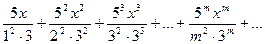

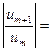


 .
. , или
, или  , или -
, или - 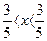 .
. '--данный ряд принимает вид
'--данный ряд принимает вид 
 . Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит,
. Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит,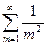 .
.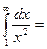
 =
=  .
. область сходимости данного ряда.
область сходимости данного ряда.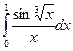 с точностью до 0,001.
с точностью до 0,001.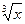 , имеем:
, имеем: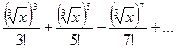
 =х
=х  -
- 
 =
=
 3-
3- 
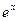 , sin x, cos x, (1+х)
, sin x, cos x, (1+х) 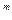 ,
,


