Контрольная работа № 1
В задачах 1—20 даны вершины треугольника АВС. Найти: 1) длину стороны АВ 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС. 1. A(—5; 0), B(7; 9), C(5; —5). 2. А(—7; 2), B(5; 11), C(3; —3). 3. А(— 5; —3), B(7; 6), С(5; —8). 4. A(—6; —2), B(6; 7), C(4; -7). 5. A(—8; —4), B(4; 5), C(2; —9). 6. А (0; —1), B(12; 8), C(10; —6). 7. A(—6; 1), В( 6; 10), C(4; —4). 8. A(—2; —4), B(10; 5), C(8; —9). 9. A(—3; 0), B(9; 9), C(7; —5). 10. A(—9; —2), B(3; 7), C(1; —7). 11. A (— 5; 2), B(7; -7), C(5; 7). 12. А(—7; 5), B(5; —4), C(3; 10). 13. A(—7; 1), B(5; —8), C(3; 6). 14. А(0; 3), B(12; —6), C(10; 8). 15. А(—8; 4), В( 4; -5), C(2; 9). 16. А(—2; 2), B(10; —7), C(8; 7). 17. A(1; 2), B(13; —7), C(11; 7). 18. А(—4; 1), B(8; —8), C(6; 6). 19. А(—7; —1), В (—5; —10), C(3; 4). 20. А(—3; 3), B(9; —6), C(7; 8). В задачах 21—25 составить уравнение линии, для каждой точки которой отношение расстояний до точки А( 21. А(4; 0), а = 9, е= 22. А(-8; 0), а =-2, е = 2. 23. А(4; 0), а=1, е=2. 24. А(9;0), а =-4, е=1,5. 25. А(-1;0), а=-4, е= В задачах 26—30 составить уравнение линии, для каждой точки которой ее расстояние до точкиА( 26. А(2;1), b=-1. 27. А(-2;-2), b=-4. 28. А(2;-1), b=2. 29. А (2;-1), b=1. 30. А(4;-1), b=1. В задачах 31—40 даны координаты точек А, В, С. Требуется: 1) записать векторы 31. А (7; —4; 1), В(12; —3; 1), С(10; 1; 5). 32. А (0; —3; 3), В(5; —2; 3), С(3; 2; 7). 33. А (—2; —1; —2), В(3; 0; —2), С(1; 4; 2). 34. А (-6; 0; 0), В(-1; 1; 0), С(—3; 5; 4). 35. А (-2; -3; -8), В(3; -2; -8), С(1; 2; -4). 36. А(,1; 0; -1), В(6; 1; -1), С(4; 5; 3). 37. А (-1;.4;1), В(4;5;1), С12; 9; 5). 38. А (3; -6; -3), В(8; —5; —3), С(6; — 1; 1). 39. А (1; 0; 0), В(6; 1; 0), С(4; 5; 4). 40. А.(2; -8; -2), В(7; -7; -2), С(5; -3; 2). В задачах 41—50 дамы векторы 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. В задачах 51—60 систему уравнений зависать в матричной форме и решить ее с помощью обратной матрицы. 51. 53. 55. 57. 59. В задачах 61—80 найти указанные пределы. 61. а) в) 62. а) в) 63. а) в) 64. а) в) 65. а) в) 66. а) в) 67. а) в) 68. а) в) 69. а) в) 70. а) в) 71. а) в) 72. а) в) 73. а) в) 74. а) в) 75. а) в) 76. а) в) 77. а) в) 78. а) в) 79. а) в) 80. а) в)
|

 ;у
;у 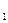 ) и до прямой х=а равно числу е. Полученное уравнение привести к простейшему виду и построить кривую.
) и до прямой х=а равно числу е. Полученное уравнение привести к простейшему виду и построить кривую. .
. .
.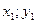 ) равно расстоянию до прямойу=b. Полученное уравнение привести к простейшему виду и построить кривую.
) равно расстоянию до прямойу=b. Полученное уравнение привести к простейшему виду и построить кривую. и
и 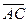 в системе орт и найти модули этих векторов; 2) найти угол между векторами
в системе орт и найти модули этих векторов; 2) найти угол между векторами 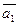 ,
,  ,
, 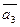 ,
,  . Показать, что векторы
. Показать, что векторы  52.
52. 
 54.
54. 
 56.
56. 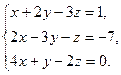
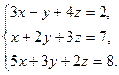 58.
58. 
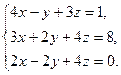 60.
60. 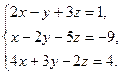
 ; б)
; б) 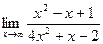 ;
; ; г)
; г)  .
.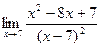 ; б)
; б)  ;
; ; г)
; г) 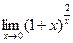 .
. ; б)
; б)  ;
;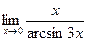 ; г)
; г) 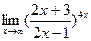 .
. ; б)
; б)  ;
; ; г)
; г)  .
.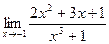 ; б)
; б) 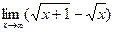 ;
; ; г)
; г)  .
. ; б)
; б)  ;
;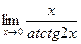 ; г)
; г) 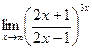 .
. ; б)
; б) 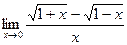 ;
;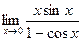 ; г)
; г) 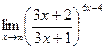 .
. ; б)
; б) 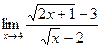 ;
;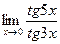 ; г)
; г) 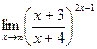 .
. ; б)
; б) 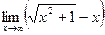 ;
; ; г)
; г)  .
.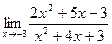 ; б)
; б) 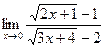 ;
; ; г)
; г)  .
.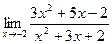 ; б)
; б)  ;
; ; г)
; г) 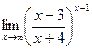 .
.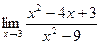 ; б)
; б)  ;
; ; г)
; г) 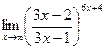 .
.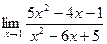 ; б)
; б)  ;
;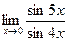 ; г)
; г) 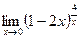 .
. б)
б) 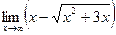 ;
;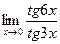 ; г)
; г)  .
.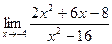 ; б)
; б) 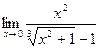 ;
; ; г)
; г) 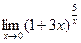 .
. ; б)
; б) 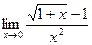 ;
; ; г)
; г)  .
. ; б)
; б)  ;
;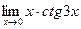 ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
;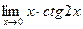 ; г)
; г) 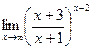 .
.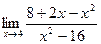 ; б)
; б)  ;
;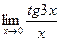 ; г)
; г) 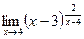 .
.


