Контрольная работа №2
В задачах 81-100 найти производные функций 81. а) у=хtgx+Lncosx+e в) 82. а) в) 83. а) в) 84. а) в) 85. а) в) 86. а) в) 87. а) в) 88. а) в) 89. а) в) 90. а) в) 91. а) в) 92. а) в) 93. а) в) 94. а) в) 95. а) в) 96. а) в) 97. а) в) Lny+xy-5=0. 98. а) в) 99. а) в) 100. а) в) В задачах 101-120 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проверить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции. 101. 104. 107. 110. 113. 116. 119. 121. Каковы радиус основания R и высота Н открытого цилиндрического бака данного объема V, чтобы на его изготовление пошло наименьшее количество листового металла? 122. Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения 18 м. При каком радиусе полукруга площадь сечения будет наибольшей? 123. Найти стороны прямоугольника наибольшей площади, который можно вписать в эллипс 124. Найти наибольший объем цилиндра, полная поверхность которого равна S. 125. Найти наибольший объем конуса, образующая которого равна L. 126. Определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала. 127. Сумма двух положительных чисел равна а. Каковы эти числа, если сумма их кубов будет наименьшей? 128. Два коридора шириной 2,4 м и 1,6 м пересекаются под прямым углом. Определить наибольшую длину лестницы, которую можно перенести горизонтально из одного коридорав другой. 129. На параболе у=х2 найти точку, наименее удаленную от прямой у = 2х —4. 130. Из всех прямоугольников, вписанных в круг радиуса R, найти тот, который имеет наибольшую площадь. В задачах 131—135 исследовать на экстремум функцию z = f(x, у). 131. 132. 133. 134. 135. В задачах 136—140 найти наименьшее и наибольшее значения функции z=f(x, у) в данной замкнутой области. 136. 137. 138. 139. 140. В задачах 141-160 найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием. 141. а) 142. а) 143. а) 144. а) 145. а) 146. а) 147. а) 148. а) 149. а) 150. а) 151. а) 152. а) 153. а) 154. а) 155. а) 156. а) 157. а) 158. а) 159. а) 160. а) В задачах 161—170 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж. 161. 162. 163. 164. у=х 165. у=-х 166. 167. 168. 169. 170. В задачах 171 —175 вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями. Сделать чертеж. 171. 172. ху=4; х=1; х=4;, у=0. 173. у=sinx (одна полуволна); y=0. 174. у=х 175. В задачах 176-180 вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной указанными линиями. Сделать чертеж. 176. 177. 178. х+у-2=0; х=0;у=0. 179. ху=2; х=0; у=1; у=4. 180.
|

 ; б)
; б)  ;
;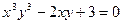 .
. ; б)
; б)  ;
;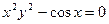 .
. ; б)
; б)  ;
;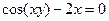 .
.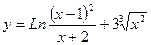 ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
.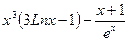 ; б)
; б)  ;
; .
. ; б)
; б)  ;
;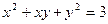 .
. ; б)
; б)  ;
; .
.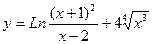 ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б) 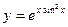 ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
.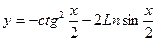 ; б)
; б)  ;
; .
. ; б)
; б)  ;
; /
/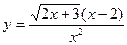 ; б)
; б) 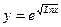 ;
;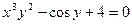 .
.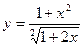 ; б)
; б)  ;
; ; б)
; б)  ;
;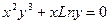 .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. . 102.
. 102.  . 103.
. 103.  .
. . 105.
. 105. 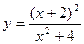 . 106.
. 106.  .
. . 108.
. 108. 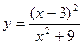 . 109.
. 109. 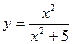 .
.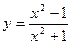 . 111.
. 111.  . 112.
. 112.  .
. . 114.
. 114.  115.
115.  .
.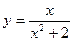 . 117.
. 117.  . 118.
. 118.  .
. 120.
120.  .
. .
.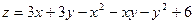 .
.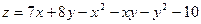 .
. .
. .
. .
. в прямоугольнике
в прямоугольнике  ,
,  .
. в треугольнике, ограниченном осями Ох и Оу и прямой у=2-х.
в треугольнике, ограниченном осями Ох и Оу и прямой у=2-х. в прямоугольнике
в прямоугольнике  ,
, 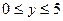 .
. в области, ограниченной параболой
в области, ограниченной параболой  и осью Ох.
и осью Ох.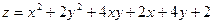 в квадрате
в квадрате  ,
, 
 ; б)
; б)  ; в)
; в)  .
.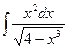 ; б)
; б)  ; в)
; в)  .
.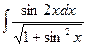 ; б)
; б) 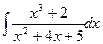 ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 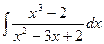 ; в)
; в)  .
. ; б)
; б)  ; в)
; в) 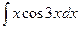 .
. ; б)
; б)  ; в)
; в) 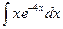 .
.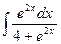 ; б)
; б) 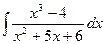 ; в)
; в)  .
.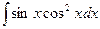 ; б)
; б)  ; в)
; в)  .
.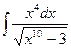 ; б)
; б)  ; в)
; в) 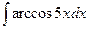 .
.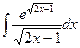 ; б)
; б)  ; в)
; в)  .
.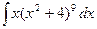 ; б)
; б) 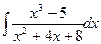 ; в)
; в) 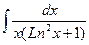 ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 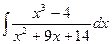 ; в)
; в) 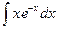 .
.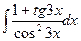 ; б)
; б)  ; в)
; в)  .
.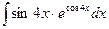 ; б)
; б)  ; в)
; в) 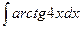 .
. ; б)
; б) 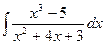 ; в)
; в)  .
. ;
;  .
. ; у=6-х.
; у=6-х.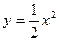 ; у=4-х.
; у=4-х.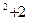 ; у=4-х
; у=4-х 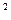 .
. ; у=х-1.
; у=х-1.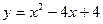 ; у=х.
; у=х. ;
;  .
.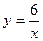 ; у=7-х.
; у=7-х.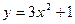 ; у=3х+7.
; у=3х+7. ; у=-х.
; у=-х. ;
;  .
. .
. ; х=0.
; х=0.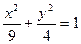 .
.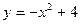 ; х=0; у=0; у=3.
; х=0; у=0; у=3.


