 гл. VI § 1-9; [3] № 683, 685, 700. 701;
гл. VI § 1-9; [3] № 683, 685, 700. 701;
 |гл. VII § 1 —13; [3] № 716, 734, 736, 738, 744, 747, 782, 789;
|гл. VII § 1 —13; [3] № 716, 734, 736, 738, 744, 747, 782, 789;
 гл. VIII; [3] № 816, 820, 825 (2, 3).
гл. VIII; [3] № 816, 820, 825 (2, 3).
Разберите решение задач 6, 7 данного пособия.
Задача 6. Вычислить пределы:
а) 
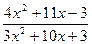 , б)
, б)  (
( ,
,
в) 
 , г)
, г) 
 .
.
Решение. а) Подстановка предельного значения аргумента х=-3 приводит к неопределенному выражению вида
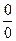 .
.
Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля трих  :
:

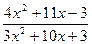 =
= 
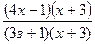 =
= 
 ;
;
б) При х  выражение
выражение  дает неопределенность вида
дает неопределенность вида  . Для ее устранения умножим и разделим это выражение на (
. Для ее устранения умножим и разделим это выражение на ( :
:
 (
( =
= 


 =
= 
 ;
;
в) Обозначим arctg 5х=у. Тогда 5х =tg у и у  при х
при х  . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела 
 , имеем:
, имеем:

 =
= 





 ;
;
г) При х  выражение
выражение  является неопределенностью вида 1
является неопределенностью вида 1  . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при х
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при х  величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела:
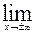
 .
.
Тогда имеем: 




 .
.
Пусть 2х+1=-4у. Тогда 4х+5=-8у+3 и у  при х
при х  . Переходя к переменной у, получим:
. Переходя к переменной у, получим:



 .
.
Задача 7. Исследовать на непрерывность функцию у = 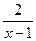 . Рис.4
. Рис.4
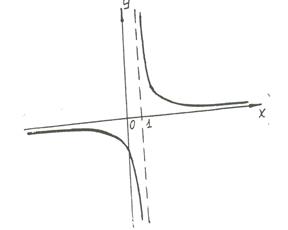
Решение. Данная функция является элементарной. Известно, что всякая элементарная функция непрерывна на своей области определения. Данная функция определена на интервалах (- 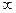 ;1) и (1;
;1) и (1; 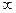 ) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 4.
) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 4.
Вопросы для самопроверки
- Сформулируйте определение понятия функции.
- Что называется областью определения функции? областью изменения функции?
- Перечислите основные элементарные функции. Назовите их основные свойства.
- Какие функции называются элементарными? Приведите примеры.
- Что называется пределом числовой последовательности?
- Сформулируйте определение предела функции.
- Назовите основные свойства пределов функций.
- Какая функция называется бесконечно малой? бесконечно большой?
- Назовите свойства бесконечно малых функций.
- Напишите формулы первого «второго замечательных пределов.
- Какие логарифмы называются натуральными?
- Дайте определения односторонних пределов функции в точке.
- Какая функция называется непрерывной в точке? на интервале?
- Какая точка называется точкой разрыва первого рода? второго рода?
- Перечислите основные свойства непрерывных на отрезке функций.

 гл. VI § 1-9; [3] № 683, 685, 700. 701;
гл. VI § 1-9; [3] № 683, 685, 700. 701;
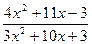 , б)
, б)  (
( ,
,
 , г)
, г)  .
.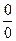 .
. :
: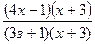 =
=  ;
; выражение
выражение  . Для ее устранения умножим и разделим это выражение на (
. Для ее устранения умножим и разделим это выражение на ( :
:
 =
=  ;
;
 , имеем:
, имеем:



 ;
; . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при х
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при х 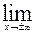
 .
.

 .
. при х
при х 

 .
.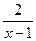 . Рис.4
. Рис.4
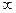 ;1) и (1;
;1) и (1; 


