ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Задача 1.Даны вершины треугольника АВС: А(—4; 8), В (5; —4), С( 10; 6)
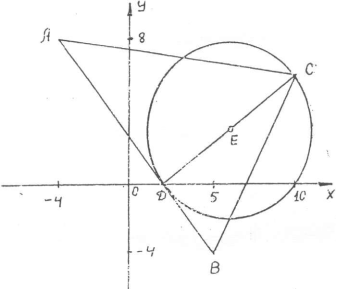
Задача 1. Даны вершины треугольника АВС: А(—4; 8), В (5; —4), С(10; 6). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АСи их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС. Решение: 1. Расстояние d между точками М 1 (х1; у1) и М2 (х2; у2)определяется по формуле
d=
Подставив в эту формулу координаты точек А и В, имеем: АВ= 2. Уравнение прямой, проходящей через точки М 1 (х1; у1) и М2 (х2; у2) имеет вид:
Подставив в (2) координаты точек А и В, получим уравнение прямой А В:
Зу—24 = —4х— 16, 4х+3у—8 = 0 (АВ). Для нахождения углового коэффициента RАВ прямой АВ разрешим полученное уравнение относительно у:
Отсюда RАВ=-
х+7у-52=0 (АС) Отсюда RАС=- 3. Угол α между двумя прямыми, угловые коэффициенты которых равны R1 и R2 определяется по формуле:
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее R1= RАВ= -
tg А=
4. Так как высота СD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т. е.
R Уравнение прямой, проходящей через данную точку М 1 (х1; у1) в заданном угловым коэффициентом к направлении, имеет вид: у-у Подставив в (4) координаты точки С и R у-6= Для нахождения длины СD определим координаты точка D, решив систему уравнений (АВ) и (СD):
откуда х=2, у=0, то есть D (2; 0). Подставив в формулу (1) координаты точек С и D, находим: CD= 5. Уравнение окружности радиуса R с центром в точке Е (a; b) имеет вид: (х-a) Так как СD является диаметром искомой окружности, то ее центр E есть середина отрезка СD. Воспользовавшись формулами деления отрезка пополам, получим: х Следовательно, Е ( 6; 3) и R= получаем уравнение искомой окружности: (х-6)
6. Множество точек треугольника АBС есть пересечение трёх полуплоскостей, первая из которых ограничена прямой АB и содержит точку С, вторая ограничена прямой ВС и содержит точку А, а третья ограничена прямой АС я содержит точку В. Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С: 4*10+3*6-8=50>0
Поэтому искомое неравенство имеет вид: 4х+3у-8 Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и. содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:
2х-у-14-0 (BC).
Подставив в последнее уравнение координаты точки А, имеем: 2*(-4)-8-14=-30<0. Искомое неравенство будет 2х—у—14≤0. Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В: 5+7*(—4)—52=-75<0. Третье искомое неравенство х+7у—52≤0. Итак, множество точек треугольника АBС определяется системой неравенств
На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АBС, высота СD, окружность с центром в точке Е.
Рис.1 Задача 2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки А(3; 0) и до прямой х=12 равно числу е = 0,5. Полученное уравнение привести к простейшему виду и построить кривую. Р е ш е н н е. Пусть М(х; у) —текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр МB на.прямую х=12 (рис. 2). Тогда B( 12; у). По условию задачи МА = Тогда
4х
Полученное уравнение представляет собой эллипс вида
Определим фокусы эллипса F
То есть, F Эксцентриситет эллипса
Задача 3. Составить уравнение линии для каждой точки которой ее расстояние до точки А(3; —4) равно расстоянию до прямой у= 2. Полученное уравнение привести к простейшему виду и построить кривую. Решение. М(х;у) —текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую у=2 (рис. 3). Тогда В{х;2). Так как МА=МВ, то
-12у-12=(х-3) у+1=-
Полученное уравнение определяет параболу с вершинойвточке 0 ' ( 3; —1). Для приведения уравненияпараболыкпростейшему (каноническому) виду положим х—3=Х', у+1= У'. Тогда в системе координат Х'О'У 'уравнениепара болы принимает следующий вид: У=- В системекоординат Х'О'У ' строим параболу. Вопросы для самопроверки
6. Как найти координаты точки пересечения двух прямых? 7. Напишите формулу для определения угла между двумя прямыми.
|


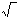
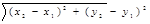 (1)
(1) .
. (2)
(2) ,
,  ,
,  ,
,
 . Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС.
. Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС. ,
,  ,
, 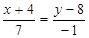 ,
, .
.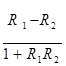 . (3)
. (3)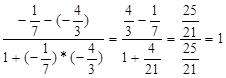 ,
, А=arctg 1=45
А=arctg 1=45 
 0,79 рад.
0,79 рад. =-
=-  =-
=-  =
= 
 =R(х-х
=R(х-х  ,
, .
.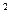 +(у-b)
+(у-b) 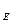 =
=  , у
, у 
 . Используя формулу (6),
. Используя формулу (6),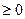
 ,
,  ,
,  ,
,
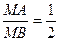 . По формуле (1) из предыдущей задачи
. По формуле (1) из предыдущей задачи , МВ=
, МВ=  .
. ,
,  ,
, , 3х
, 3х 
 .
. где а=6, b=3
где а=6, b=3  .
.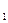 (-с;0) и F
(-с;0) и F  (с;0). Для эллипса справедливо равенство b
(с;0). Для эллипса справедливо равенство b 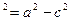 , откуда
, откуда и с=3.
и с=3. =
=  .
.
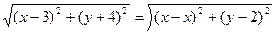 или
или ,
, .
.
 Х')
Х') 


