[5] гл. XXI; [3] № 592, 624, 628.
Разберите решение задачи 5 данного пособия.
Задача 5. Данную систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:

Р е ш е н и е. Обозначим через А — матрицу, коэффициентов при неизвестных; X — матрицу-столбец неизвестных  ; Н — матрицу-столбец свободных членов:
; Н — матрицу-столбец свободных членов:
А=  , Х=
, Х=  , Н=
, Н= 
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
А*Х=Н. (1)
Если матрица А — н е в ы р о ж д е н н а я (ее определитель  отличен от нуля), то она имеет обратную матрицу А
отличен от нуля), то она имеет обратную матрицу А  . Умножив обе части уравнения (1) на А
. Умножив обе части уравнения (1) на А  , получим:
, получим:
А  *А*Х= А
*А*Х= А  *Н.
*Н.
Но А  *А=Е (Е — единичная матрица), а ЕХ=Х,.поэтому
*А=Е (Е — единичная матрица), а ЕХ=Х,.поэтому
Х=А  *Н (2)
*Н (2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А 
Пусть имеем невырожденную матрицу
А=  . Тогда А
. Тогда А  =
=  ,
,
где А  (i=1,2,3; j=1, 2, 3) —алгебраическое дополнение элемента а
(i=1,2,3; j=1, 2, 3) —алгебраическое дополнение элемента а  в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) второго порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А.
в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) второго порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А.
Вычислим определитель  и алгебраические дополнения А
и алгебраические дополнения А  элементов матрицы А.
элементов матрицы А.
 =10
=10  - следовательно матрица А имеет обратную матрицу А
- следовательно матрица А имеет обратную матрицу А  .
.
 ,
,  ,
,
 ,
,  ,
,
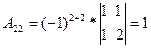 ,
,  ,
,
 ,
, 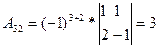 ,
,
 .
.
Тогда
А  =
=  =
=  .
.
По формуле (2) находим решение данной системы уравнений в матричной форме:
Х= А  *Н=
*Н=  .
.
Отсюда х 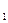 =3, х
=3, х  =0, х
=0, х  =-2.
=-2.
Вопросы для самопроверки
- Что называется определителем второго, третьего, п- го порядков?
- Назовите основные свойства определителей.
- Что называется минором, алгебраическим дополнением элемента определителя?
- Напишите формулы Крамера решения системы линейных уравнений. В каких случаях их можно использовать?
- Назовите схему решения системы линейных уравнений по методу Гаусса.
- Что называется матрицей?
- Как определяются основные действия над матрицами?
- Какая матрица называется обратной по отношению к данной матрице? Как найти матрицу, обратную данной?
- Что называется рангом матрицы? Как найти ранг матрицы?
- Сформулируйте теорему Кронекера-Капелли.
- Опишите матричный способ решения системы линейных уравнений.
- Какова геометрическая интерпретация систем линейных уравнений и неравенств?


 ; Н — матрицу-столбец свободных членов:
; Н — матрицу-столбец свободных членов: , Х=
, Х=  , Н=
, Н= 
 отличен от нуля), то она имеет обратную матрицу А
отличен от нуля), то она имеет обратную матрицу А  . Умножив обе части уравнения (1) на А
. Умножив обе части уравнения (1) на А  . Тогда А
. Тогда А  ,
, (i=1,2,3; j=1, 2, 3) —алгебраическое дополнение элемента а
(i=1,2,3; j=1, 2, 3) —алгебраическое дополнение элемента а  =10
=10  - следовательно матрица А имеет обратную матрицу А
- следовательно матрица А имеет обратную матрицу А  ,
,  ,
, ,
,  ,
,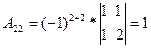 ,
,  ,
, ,
, 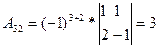 ,
, .
. =
=  .
. .
. =3, х
=3, х  =0, х
=0, х  =-2.
=-2.


