Молекулярно-массовое распределение полимера при поликонденсации
Рассмотрим молекулярно-массовое распределение полимера, полученного поликонденсацией мономера ARB или эквимолярной смеси ARA и BR1B. Используем статистический метод, который сводится к расчету вероятностей содержания в полимере макромолекул различной длины. В силу закона больших чисел эти вероятности равны численным долям Qn следовательно, подобный анализ приводит к числовой дифференциальной функции распределения. Предполагается, что все реакции между А и В равновероятны, т.е. не зависят от молекулярной массы n-меров. Макромолекула, содержащая p звеньев мономера ARB, образуется в том случае, когда прореагируют (p -1) групп А, а одна конечная группа останется непрореагировавшей. Вероятность того, что группа А в реакционной смеси окажется прореагировавшей, равна степени завершенности реакции X, непрореагировавшей - (1 - X). Отсюда:
Таким образом, среднечисловые и среднемассовые дифференциальные функции распределения полимеров, полученных поликонденсацией со степенью завершенности X, описываются выражениями (5.111) и (5.115). При X = 1 обе функции не определены, поскольку теоретически в этом случае образуется одна гигантская макромолекула. Выражения для средних степеней полимеризации могут быть легко получены, исходя из их определения. Ранее показано, что
где
Ряд (5.116) является сходящимся, так как X < 1, его сумма равна
Это уравнение, называемое уравнением Карозерса, было получено ранее (5.92). Далее рассмотрим среднемассовую степень полимеризации
где Qw - массовая доля макромолекул со степенью полимеризации р. Совмещая (5.115) с (5.116), получаем:
Сумма этого ряда равна:
Согласно определению параметра полидисперсности,
Из (5.119) следует, что в процессе поликонденсации ширина распределения возрастает, при этом параметр полидисперсности стремится к двум, что характерно для наиболее вероятного распределения Флори.
|


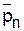 = ∑pQn
= ∑pQn








