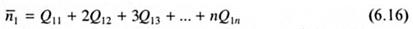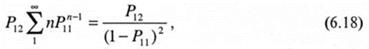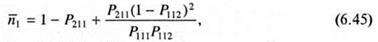Состав и микроструктура сополимера. Статистический подход
Уравнения состава сополимера могут быть получены более строгим -статистическим методом без каких-либо исходных допущений, как это было сделано выше, которые предполагают равенство скоростей перекрестного роста. Кроме того, этот метод позволяет количественно охарактеризовать микроструктуру цепи случайных и статистических сополимеров. Один из вариантов такого описания предложен Алфреем и Голдфинером, которые рассчитали вероятности образования последовательностей одинаковых звеньев разной длины, т.е:
Очевидно, что вероятности образования тех или иных последовательностей звеньев в цепи равны произведению вероятностей соответствующих элементарных актов. Вероятность той или иной элементарной реакции равна ее скорости, деленной на сумму скоростей всех элементарных реакций с участием рассматриваемого типа активного центра. При бинарной сополимеризации возможны лишь две реакции роста с участием каждого из типов активных центров. Тогда вероятности реакций мономеров М1 и M2 с растущими цепями, оканчивающимися мономерным звеном М1, описываются следующими соотношениями:
Вероятности Р12 и аналогичная ей Р21, которая будет рассмотрена далее, называются переходными вероятностями, так как в результате соответствующих реакций меняется природа конечного звена растущей цепи. Обозначим вероятность образования последовательности, содержащей n звеньев М1, как Q1n. Тогда, исходя из сказанного выше:
Очевидно, что при большом числе последовательностей в макромолекулах сополимера величина Q\n равна доле данных последовательностей из мономера М1. Это следует, в частности, из того, что:
с учетом Р11 < 1. Относительное содержание мономера M1 в последовательностях по отношению к его общему количеству определяется следующим образом:
Важное значение имеет такая характеристика, как среднее содержание звеньев в последовательности
или с учетом (6.13)
Поскольку
окончательно получаем:
Аналогичные соотношения могут быть получены для последовательностей из мономера М2:
Полученные исходя из простой теории вероятности соотношения позволяют получить уравнение состава сополимера, а также количественно охарактеризовать его микроструктуру. Первое может быть сделано практически сразу через уравнение Голдфингера, которое получается делением (6.19) на (6.24):
Подставив в (6.25) выражения (6.11) и (6.21), окончательно имеем:
где Y = F1/F2 = Δ[M1]/Δ[M2], X = ƒ1/ƒ2 = [M1]/[M2]. Уравнения (6.5), (6.6) и (6.27) легко переходят друг в друга, т. е. идентичны. Вернемся к микроструктуре сополимера. В табл. 6.1 приведены данные по относительному содержанию гомопоследовательностей, т. е. последовательностей, состоящих из мономеров одного типа для случайного и статистического сополимеров. Из табл. 6.1 видно, что в статистическом сополимере по сравнению со случайным больше относительное содержание одиночных звеньев. Особенно это заметно для сополимеров, при образовании которых преобладает перекрестный рост вследствие r1 < 1, r2 < 1. Микроструктура сополимера количественно характеризуется его триадным составом, экспериментально определяемым методом ЯМР. Поскольку триады 112 и 211 или 221 и 122 методом ЯМР неразличимы, то обычно находится их суммарное содержание. Используя изложенный выше подход, для триад, центрированных Мi, можно показать:
при F111+F112 + F211+F212= 1. Аналогичные выражения могут быть получены для триад, центрированных М2. Исключая концентрации мономеров из уравнений (6.10), (6.11) и (6.25), можно получить соотношение:
из которого следует, что микроструктура сополимера заданного состава определяется произведением относительных активностей мономеров, а не их раздельными значениями. Модель предконцевого звена. Согласно этой модели, необходимо учитывать восемь элементарных реакций роста:
Вероятности этих реакций описываются, как обычно, отношением скорости рассматриваемой реакции к сумме скоростей обеих возможных реакций роста:
Уравнение состава сополимера наиболее просто может быть получено статистическим путем. Согласно данной модели, среднее содержание звеньев М\ в последовательностях из этого мономера выражается рядом:
который легко преобразуется в сходящийся ряд:
Учитывая что:
имеем:
что приводит, после незначительных преобразований, к конечному результату:
Аналогичным образом приходим к выражению:
и далее к уравнению, связывающему состав сополимера с переходными вероятностями:
Это уравнение является аналогом уравнения Голдфингера, рассмотренного ранее. Уравнение, связывающее состав сополимера с составом сомономерной смеси, получается путем подстановки в (6.48) выражений для вероятностей (6.34), (6.35), (6.38), (6.39):
Переходя к мольным долям для характеристики состава мономерной смеси, после незначительных преобразований, окончательно получаем:
При радикальной сополимеризации 1,2-дизамещенных этилена (М2) обычно r2 = 0. В таких случаях уравнение (6.50) трансформируется в более простое:
Микроструктура сополимера. Триадный состав сополимера, согласно модели предконцевого звена, описывается выражениями:
|



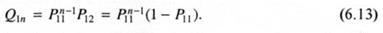


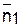 или средняя длина последовательности. Она является средневзвешенной величиной
или средняя длина последовательности. Она является средневзвешенной величиной