Виды обобщающих показателей
Абсолютные показатели характеризуют общую численность изучаемой совокупности (например, число предприятий) и общий объем признака, отражающий уровень развития изучаемого явления (например, объем произведенной продукции), то есть они отражают либо суммарное число единиц, либо суммарное свойство объекта. Все абсолютные величины являются именованными, измеряются в конкретных единицах (чел., шт., кВт-часах и т.д.), могут быть как положительными, так и отрицательными (убытки, потери и т.д.). Абсолютные показатели бывают по способу их измерения: · натуральные (килограмм удобрения); · условно-натуральные (удобрения, измеряемые в количестве действующего вещества); · стоимостные (цена за килограмм удобрения). Кроме абсолютных показателей, получаемых непосредственно в результате сводки статистических данных, применяются также абсолютные показатели, получаемые расчетным путем. Относительные показатели выражают количественные соотношения между собой абсолютных или других показателей, один из которых принят за базу сравнения. При сопоставлении базисная величина, взятая за основу для сравнения, приравнивается к удобным для использования и легко воспринимающимся числам – единиц, ста, тысячи и т.д., а сравниваемая величина соответственно преобразовывается. В зависимости от того, к чему приравнивается базисная величина, различают формы относительных величин: доля или коэффициент (базис =1), процент % (базис = 100), промилле 0/000 (базис =)1000, продецимилле 0/0000 (базис = 10 000). Показатели выполнения плана применяются для характеристики степени выполнения плана и исчисляются путем деления величины фактического выполнения на величину планового задания. Показатели структуры –это относительная доля (или удельный вес) части в целом, выраженная в %. Если исследуемая совокупность дифференцирована по одному признаку, например, работники по стажу работы, то при расчете показателей структуры по отношению к общему итогу получают простой структурный ряд. При дифференцировании по двум признакам (допустим, группы по стажу, в свою очередь, разбиты на подгруппы по возрасту) получают комбинированные структурные ряды. Структура (строение, расположение) – распределение в определенном соотношении различных частей изучаемого объекта. Показатель структуры (доля) рассчитывается как отношение отдельной части изучаемого объекта к общему объему объекта. Линейный коэффициент абсолютных структурных сдвигов:
где
Квадратический коэффициент абсолютных структурных сдвигов:
Индекс различий (имеет, в отличие от линейного и квадратического коэффициента абсолютных структурных сдвигов, и верхнюю, и нижнюю границы изменения).
где Все признаки должны быть сопоставимыми, поэтому при расчете показателей структуры отдельных объектов (состоящих из несоизмеримых по качеству элементов), физические размеры необходимо переводить в условно-сопоставимые. Например, при расчете структуры общего поголовья животных, физические головы переводятся в условные путем перемножения на соответствующие коэффициенты, то же самое при анализе тракторного парка, наличия сельхозмашин и т.д. Пример 1. Имеются данные о плановом задании и фактическом выполнении объема продаж хозяйством продовольственных товаров за два года
Таблица 1
Рассчитать: 1. Показатели выполнения плана, по каждому виду товара, и в целом. 2. Показатели структуры по фактическому объему продаж, за два года. · Относительную долю. · Линейный коэффициент абсолютных структурных сдвигов. · Квадратический коэффициент абсолютных структурных сдвигов. · Индекс различий. Решение. 1. Процент выполнение плана рассчитывается как отношение фактически выполненного объема к плановому заданию, результаты приведены в табл.2. Таблица 2
2. Для расчета показателей структуры фактических продаж рассчитаем относительные доли Рассчитаем линейный коэффициент абсолютных структурных сдвигов:
где: Таблица 3.
Рассчитаем квадратический коэффициент абсолютных структурных сдвигов:
Удельные веса отдельных видов товаров отличаются в среднем на 5,77процентных пункта по линейному показателю структуры, и на 6,14 процентных пунктов по квадратическому показателю. Индекс различий показывает на сколько структура изменилась в отчетном году по сравнению с базисным, он равен:
Показатели сравнения – сопоставление двух структурных рядов, один из которых характеризует соотношение частей совокупности по численности, а другой – по размерам какого-либо признака этих единиц. Они характеризуют степень неравномерности распределения признака в совокупности, его дифференцированию и поэтому получили название показателей дифференцирования. Показатели динамики (темпы) служат для характеристики изменения явления во времени. Рассчитывают путем отношения величины текущего периода к величине одного из прошлых периодов. При этом величину одного из прошлых периодов, который называется базисным, принимают за сто или единицу, а показатели последующих лет выражают в процентах или коэффициентах к базисному. Относительные показатели динамики называются темпами. Показатели интенсивности выражают соотношение разноименных признаков одной и той же совокупности, находящихся в определенной связи друг с другом. Например, соотношение численности населения страны с ее территорией и объемами произведенной продукции или соотношение объемов факторов производства (стоимости основных средств, числа работников, земельной площади, и т.д.) между собой и произведенной продукцией. Относительные показатели, характеризующие взаимосвязи между разными признаками объекта, объектом и средой и т.д., выражают связь, соотношение между вариацией одних (факторных) и других (результативных) признаков. Показывают, какая доля или величина вариации результативного признака приходится на единицу вариации факторного признака. Эти показатели выражаются как отвлеченными, так и именованными числами. К ним относятся: 1) коэффициенты регрессии; 2) эластичности; 3) детерминации; 4) корреляции; 5) аналитические индексы
|

 , (3.1)
, (3.1) - удельные веса (в %) отдельных частей изучаемого объекта за отчетный и базисный период;
- удельные веса (в %) отдельных частей изучаемого объекта за отчетный и базисный период; - число выделяемых частей.
- число выделяемых частей. (3.2)
(3.2) (3.3)
(3.3) - показатели удельного веса, выраженные в долях, за отчетный и базисный период.
- показатели удельного веса, выраженные в долях, за отчетный и базисный период.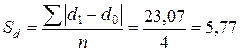 процентных пункта.
процентных пункта. - число выделяемых частей.
- число выделяемых частей.




 процентных пункта.
процентных пункта.



