Предельные вероятности системы. Уравнения Колмогорова

Одним из основных отечественных исследователей в ТМО с абстрактной точки зрения является академик Колмогоров. Считается что именно ему принадлежит основная методика оценки предельных вероятностных состояния системы.

В первые систему исследования сведения сетей использовал Леонард Клейнрок.

В настоящее время один из основных иследователей в нашей стране является Вишневский «Теоретические основы анализа систем».

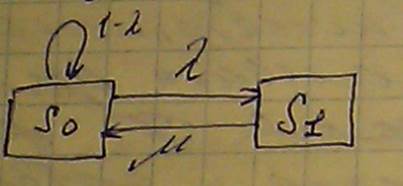
Учитывая формулу полной вероятностибудемс считать по формуле полной вероятности. Поулчим отношение

P(t+Δ t)/Δ t представляет собой производную от вероятности данного события, а в установившемся режиме любая производная будет равна 0. Поэтому можно определить формальные правила написание системы уравнений Колмогорова по графу состояний и переходов. Всего в системе уравнений Колмогорова должно быть N+1 уравнение, где n уравнений соответствуют m состояниям системы n+1 уравнение нормирвоки, т.е сумма всех вероятностей равна 1. Влевой части каждого уравнения размещается производная от вероятности данного состояния, а вправой части алгебраическая сумма вероятности, причем если стрелка для данного события является входящей, то данная вероятность берется со знаком плюс, если исходящая со знаком минус, особенность решения системы д.у. заключается в том, что для их решения необходимо определить некоторые начальные условия. Эти начальные условия каждый раз вытекают из физического смысла решаемой задачи, если мы решаем задачу об оценке коэффициента готовности резервируемой системы, то естественно предположить, что P0(0)=1, а остальные вероятности P1(0) и др=0.

Уравнения Колмогорова позволяют вычислять все состояния системы как функции времени. Особый интерес представляют собой процессы у которых есть финальные вероятности, при этом если процесс эргодический, т.е. из любого состояния системы всегда можно перейти в любое другое состояние системы за конечно число шагов, то у такой системы всегда существуют финальные вероятности.

Пример

Пусть система массового обслуживания формально представляется графом состояний и переходов:

 

Достоинством методики является то, что так, как мы вычисляем как правило только финальные вероятности, то сами производные влевой части каждого уравнения кроме уравнения нормировки будут равны 0 и система преобразуется в алгебраическу СУ, решение которой непредставляет труда. Если требуется вычислить нетолько финальные вероятности, но и сами вероятности как функции времени приходится решать систему ДУ.

 

Вычисление вероятностей состояний как функций времени(в переходный период)

Для исследования надежности эксплуатации персонального компьютера.

Рассмотрим 3 основных состояния компьютера:

S1 – исправен, но не находится в эксплуатации

S2 – исправен и находится в эксплуатации

S3 – не находится в эксплутации вследствие отказа

Введем допущение, компьютер может выходит из строя когда он находится в стадии эксплуатации.

В случае отказа компьютера его восстановление не осуществляется. Будем считать, что изменения плотности вроятности переходов пренебрежимо малы и практически не зависят от времени. При этом учитывается, что промежуток времени в течении которого учитывается надежность компьютера невелик, чтобы получить характеристики переходного периода.

Математическое описание составления размеченного графа.