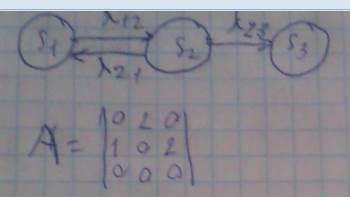
Пример 123

требуется вычислить вероятности нахожединя системы в состояниях 1,2,3 как функцию времени в момент t=1час.

Если предполагать, что в момент t=0 P1(t)=1, P2(t)=0, P3(t)=0

 

Вывод: получены 4 частных решения задачи Коши, общее решение задачи Коши получается из суммы этих решений.

P1(t)=C1P1(t)+C2(P1(t)

P2(t)=C1P2(t)+C2P2(t)

P1(t)=C1e^-4t+C2e^-t

P2(t)=-2C1e^-4t+C2e^-t (6)

Где с1,с2 произвольные константы.

Для того, чтобы получить частное решение исходной системы уравнений Р1(0)=1,Р2(0)=0, t=0,необходимо рассчитать С1 и С2.

Подставив начальные условия в су (6). Рассчитаем С1,С2.

C1=1/3

C2=2/3

Р3 из уравнения нормировки. Уравнения примут вид:

Рассматривая ф-ии времени можно показать, что графики изменения искомых вероятностей будут иметь:

 

 

Построив такие графики можно получить вероятности в любой момент переходного процесса.

 

Потоки Пальма и Эрланга

Все что рассматривали до сих пор, в т.ч. и методика оценки искомых вероятностей и их изменение в переходный период принципиально строго только в том случае, если потоки событий являются простейшими, т.е. удовлетворяют 3м условиям:

1. Стационарности
2. Ординарности
3. Отсутствие последействия

Таким трем условиям удовлетворяют только потоки, для которых время между событиями распределено экспоненцильно. Такие потоки называются Пуассоновскими Стационарными Потоками, а процессы происходящие в таких системах являются Марковскими.

Значительная часть всех практических задач может быть достаточно приближенно описана Марковскими процессами. В данном случае Марковскими процессами с дискретными состояниями и непрерывным временем.

Но на практике ряд задач не может быть описан простейшими потоками в чистом виде.

Существует ряд потоков, которые тем или иным способом могут быть сведены к простейшим, следовательно такие системы можно исследовать с помощью математического аппарата марковских цепей.

К таким потокам в первую очередь относятся потоки с ограниченным последействием. (для простейших потоков характерно отсутствие последействия)

Поток событий называется потоком с ограниченным последействием, если случайные величины T1,T2,…,Tn представляющие собой интервалы времени между 1ым и 2ым, 2ым и 3им, n и n+1 и т.д являются независимыми.

Понятие независимости характерно для всех вероятностных систем.

Потоки, для которых характерно ограниченное последействие называются потоками Пальма.

У потока Пальма случайные величины T1,T2,…,Tn имеют 1 и тот же закон распределения. С точки зрения этого определения простейший поток так же является потоком Пальма, т.к. у него случайные интервалы времени между возникновениями событий распределены по единому экспоненциальному закону и в то же время являются независимыми вв следствие выполнения последействия.

Нестационарный (интенсивности зависят от времени) не является потоком Пальма.

Частным случаем потока Пальма являются потоки Эрланга. Потоки Эрланга разделяются на потоки 1,2,3..к-ого порядка. Потоком Эрланга к-ого порядка называется поток, получающийся сохранением каждого к-ого события. Тогда поток Эрланга 1ого порядка по существу представляет собой простейший поток. А для потока Эрланга 2ого порядка характерно сохранение каждого второго события.

Т.к. у простейших потоков время между событиями распределено по одинаковому, конкретно экспоненциальному закону, то у потока Эрланга получающегося просееванием простейшего потока события между интервалами T1,T2,…,Tn так же будут иметь одинаковое распределение. Для случайной величины Tk-ое для интервала времени между двумя любыми соседними событиями у потока Эрланга k-ого порядка порожденного простейшим потоком с интенсивностью лямбда основные характеристики будут определяться:

1. плотность распределения

,где t>0, k=1,2,3 И тд

2. математическое ожидантие

3. дисперсия

4. средне квадратическое отклонение

 

Закон распределения с плотностью описываемой выражением 1 называется законом Эрланга к-ого порядка с параметром лямбда.

Степень вырождаемости определяется формулой лямбда/лямбдаt

Поток Эрланга получается из простейшего потока путем просеивания каждого k-ого события, следовательно интенсивность потока Эрланга k-ого порядка определяется как отношение лямбда/k. Лямбда – интенсивность простейшего потока, из которого к-ым просеиванием получается поток Эрланга.

Интенсивность потока Эрланга к-ого порядка в к раз меньше интенсивности простейшего потока, из которого он получен. Такое уменьшение интенсивности потока приводит к проблемам использования потоков Эрланга к-ого порядка при моделировании событий в том числе и в процессе принятия решений.

Для решения этой проблемы в теории массового обслуживания введены т.н. нормированные Эрланговские потоки. Тогда при моделировании потоков событий Эрланговский поток к-ого порядка заменяют нормированным Эрланговским потоком с тем же мат.ожиданием и дисперсией интервала времени между двумя ближайшими событиями. Для того, чтобы перейти от потока Эрланга к нормированному потоку Эрланга используют искуственный прием, т.е. уменьшают по оси 0 t масштаб в к раз, образованный таким образом поток Эрланга к-ого порядка называют нормированным и обозначают Эрланговский поток к-ого порядка Э с чертой(к).

Учитывая такой прием для нормированного эрлангова потока к-ого порядка будут определены характеристики:

1. Интенсивность потока. Лямбда (к) с чертой=к*лямбда(к)
2. Мат.ожидание.

1. Среднеквадратическое отклонение – сигма с чертой.

Потоки Эрланга в классе потоков Пальма обладают достоинство, что их использование позволяет осуществлять формальный переход от немарковских процессов к марковским, для которых в настоящее время достаточно хорошо разработан научно-методический аппарат.