Циклические ветвящиеся процессы
При исследовании и принятии решений с помощью автоматизированных информационных систем приходится использовать циклические ветвящиеся процессы. Циклическими называются процессы граф состояий и переходов, которых имеет вид.
циклический процесс вырождается в процесс гибели и разможения. На практике среди циклических процессов особо выделяют циклический ветвящийся процесс. Выделяют циклические и ветвящиеся процессы, у которых граф состояний и переходов имеет следующий вид:
Характерно, что в некоторой вершине Sn последовательно протекающий процесс с дискретными состояниями и непрерывным временем начинает ветвиться в k вершин с некими вероятностями qi, где сумма этих вероятностей равна 1. После исполнения некоторых действий в параллельных вершинах Sm+1 Sm+i Все ветвящиеся процессы сходятся в одну вершину Sm+i+1. В теории массового обслуживания доказано, что в этом случае вроятности всех дискретных состояний Pk При планировании расходов на ремонт ПК некоторой организации обычно представляют интерес следующие его состояния: S1 – пк исправен и работает S2 – пк не исправен и осуществляется поиск неисправностей S3 – неисправность обнаружена, оказалась несущественной и устраняется силами самой, использующей пк организации. S4 – неисправность обнаружена, оказалась существенной и для ее устранения требуется приглашение специалиста из организации обслуживающей компьютеры. S5 - неисправность устранена, ведется подготовка компьютера к включению Требуется оценить вероятности нахождения системы во всех состоянияхи в первую очередь в S4, оценив при этом цену работы приглашенного специалиста. Предположив при этом: процесс протекающий в системе является дискретным марковским процессом с дискретными состояниями и непрерывным временем, т.е. процессы отказа компьютера и его восстановление считаются простейшими. В расчет принять что среднее время Т1 с чертой – среднее время безотказной работы компьютера и равно 1,5 суток. Т2 Среднее время поиска неисправности равно 1 час.Т3 Среднее вемя устранения отказа пользователем равно 4 часа. Среднее время восстановления пк специалистом из обслуживающей организации Т4= 6 часов. Среднее время подготовки компьютера после отказа Т5 45 минут. Неисправность компьютера может быть устранена силами пользователя с вероятностью Q=0.65 1 час работы специалиста из обслуживающей организации оплачивается в размере равна 200р.
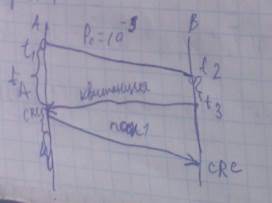
Применение математического аппарата для параллельных конечных марковских цепей для оценки доставки сообщений в компьютерных сетях Во всех современных протоколах доставки сообщений используется обратная связь, при этом формально процесс доставки фрейма, кадра, пакета можно представить следующим образом: Имеются 2 абонента в нек. Момент времени T1 абонент А формирует пакет данных, он поступает в В во время t2. T1-t2 определяется средой, способами обработки, а надежность доставки в основном характеризуется длиной передаваемого пакета, моделью использованного канала связи и параметрами этой модели. Предположим, что пакет данных передается по радиоканалу в системе вайфай. При этом модель канала биномиальная, веротяность искажения элементарно символа P0=10^-3.
С целью повышения надежности и верности доставки пакетов сообщений каждый пакет снабжается контрольной суммой
Lp=1000 Представляющая собой хэш сумму. Таким образом пакет данных имеет структуру заголовок, пакет данных и crc. Тогда если P0 – вероятность искажения одного символа в пакете сообщения, то вероятность доведения пакета с одного повтора будет определяться как Рn=(1-Р0)^Lф Рn=0,368 Тогда на приемной стороне принятый пакет подвергается обработке, расчитывается crc и сравнивается с crc в полученном пакете. Если crc рассчитаная в пункте В и crc принятая в пакете совпадают, то считается, что пакет принят верно. Сторона В отправляет свою crc и сторона А считает свою crc, если совпадает с полученным значением, то считается, что квитанция доведена и передача пакета прекращается. Если сторона В при вычислении crc обнаруживает несовпадение crc пакета или сторона А обнаруживает не совпадение crc квитанции, то в зависимости от особенностей протокола передачи с ожиданием или с непрерывной передачей абонент А, не дождавшись квитанции в течении таймаута, передает тот же пакет данных вторично. Повторяется, пока не будет истрачено заданное количество повторов, которое вычисляется аналитически. Каким образом принять решение на установление числа повторов, чтобы вероятность доведения пакетов сообщения была бы нениже требуемой, для ответа на этот вопрос используют математический аппарат дискретных конечных марковских цепей. Первая часть этого матаппарата во много повторяет матаппарат теории массового обслуживания, но так как марковский процесс с дискретным состоянием и дискретным временем описывается вероятностями, а не интенсивностями, то в этом случае дуги соединяющие состояние системы будут раскрашены соответствующими вероятностями. Предположим, что осуществляется одна попытка передачи пакета, тогда граф состояний и переходов примет вид:
S0 – абонент А сформировал и передает пакет данных Тогда с Р01=0,368 этот пакет будет доведен до S1 С Р00=1-Р01 будет не доведен Р12 будет доведена до абонента А 1-Р12 не будет доведена до А Если А получил квитанцию и алгоритм получения crc выполняется, то это характеризуется вероятностью Р22=1 Состояние S2 называется поглащающим В процессе длительной передачи в таком графе будут возникать финальные вероятности Р0,Р1,Р2 Р2 будет определять вероятность доведения пакета сообщений. Такой процесс описывается матрицей состояний и переходов, в данном случае это будет: P[2,2]=
=
В дальнейшем расчет вероятностей осуществялется с помощью уравнений Колмогорова-Чепмена, которое имеет вид: Р[I]=P(0)*P[n,n] P(I) – вероятность нахождения системы в и-ом состоянии Р(0) – вектор исходного состояния Р[n,n] – матрица переходов и состояний в степени i, так как операция возведения в степень матриц является неудобной для программирования и работы компьютеров, то уравнение Коломогорова-Чепмена переписывают в виде итерационной процедуры. Р[I]=P[I-1]*P[n,n] P[I] – вероятность нахождения системы в i-ом состоянии P[I-1] – веротяность нахождения в предыдущем состоянии Р[n,n] – невозводимая в степень I Р(0)=<1 0 0> P[1]=P(0)*P[n,n] P[1]=
Матрица переходов состояний является стохастической – сумма элементов строки равна 1. Следовательно все остальные будут давать 1. Предположим требуется вероятность доведения 0,99 Р[2]=P[1]*P[n.n]=<0.399, 0.433. 0.233> И пока не получим нужную точность
Элементы статистической теории принятия решений Рассмотренные ранее вопросы касались только. Как правило для принятия решения в таких системах используются основные положения статистическойй теории принятия решений. Рассмотрим элементы этой теории на примере системы передачи компьютерной информации. 2 или несколько компьютеров связываются между собой через элементы компьютерной сети, базовой основой которой являются элементы сети связи, если базовая сеть связи является аналоговой, то основным показателем качества такой связи является отношение сигнал/шум между народная транскрипция SNR. В русской h0^2 представляет собой отношение средней мощности сигнала к средней мощности помех(Pc штрих/Pnштрих). В настоящее время все системы переводят на цифровую связь, для которых аш 0 квадрат неприменима. Необходимо было найти аналог к записи h0^2 и получил обозначение Q=Eb/N0 Е битовое – энергия сигнала несущего один бит информации. N0 – спектральная плотность мощности шума. Eb=S*Iс S мощность сигнала Ic длительность N0=N/W N мощность шума W ширина канала. Q=S*Tc/(N/W) Битовая скорость передачи противоположна длительности сигнала, то после всех преобразований, что Q как нормированное отношение сигнал шум выглядит q=S/N * W/R Q(SNR,R зависит от двух параметров – нормированное отношение сигнал шум и от скорости передачи данных в канале Качественно зависимость вероятности искажения элементарного символа или бита информации от нормированного отношения сигнал шум имеет вид. Рис1 При значения q>q’ вероятность искажения элементарного символа будет меньше, чем некоторое допустимое Р’0. Это позволяет утверждать, что для качественного приема сигнала в цифровой системе связи нужно уметь различать все передаваемые сигналы по отношению сигнал шум. Необходимо отметить, что как и h0^2 нормированное отношение q является величиной безразмерной. Это позволяет в устройстве выборки сигнала устанавливать некий безразмерный порог, т.е величину и говорить о том, что если принимаемый сигнал по какому-то параметру превышает заданный порог, а все остальные сигналы порога не превышают, то с некоторой вероятностью можно утверждать, что передавался именной iый сигнал. Тогда процесс демодуляции и декодирвания реализуемый на приемной стороне в автоматическом режиме будет состоять из двух отдельных этапов:
В общем виде критерий описанный выражением имеет вид: Z(t)=H1> <H2=гамма. Н1,Н2 – гипотезы передачи сигналов Н1 и Н2 соответственно. Тогда критерий можно читать следующим образом: «если полученный сигнал превышает некоторое значение порога гамма, то можно принять решение в пользу гипотезы Н1. Если не превышает, то в пользу гипотезы Н2. Рассчитаны на минимизацию ошибки. Критерий подобия для двоичных сигналов имеет вид: P(z/s1)/P(z/s2)=H1> <H2=P(s2)/P(s1) P(s1),P(s2) – априорные вероятности передачи сигналов в S1,S2 Такое правило означает, что если отношение функций правдоподобия больше отношения априорных вероятностей, то решение необходимо принять в пользу гипотезы Н1, иначе в пользу гипотезы Н2. В тех случая наиболее часто используемых, когда вероятности двоичных символов равны между собой формула вырождается в: Z(t)=H1> / <H2=(a1+a2)/2=Гамма 0. А1,а2 – фрагменты априорно передаваемых сигналов Гамма0 – некий оптимальный порог для минимизации ошибки. Такой критерии в теории статистических решений называют критерием минимальной ошибки. Если сигналы явновероятны, то оптимальный порог гамма0 проходит через пересечение функций правдоподобия. Это можно графически изобразить: рис2 на мобиле С точки зрения математики – функции плотности вероятностей. Если предположить, то детектор приемника выглядел некий сигнал со значением z0(t), то приемному устройству принимающему решения достаточно высчитать эти компоненты. В данном случае x2>x1, то устройство принятия решения принимает решение в пользу S1. Сам детектор и его устройство выделения сигнала упрощаются. Если предположить, что сигналы равновероятны, а вероятность искажения 1 в 0 и 0 в 1 примерно равны, то для того, чтобы высчитать одну из составляющих ошибки необходимо рассчитать площадь хвоста от – бесконечности до гамма0. Это будет вероятность ложного приема сигнала. Такую ошибку называют ошибкой первого рода. Если серьезно загрубить устройство выделения сигнала, то это может привести к тому, что сигнал не будет принят вообще, то есть получим вероятность пропуска сигнала или ошибку второго рода. Как правило при создании детекторов приемных устройств в первую очередь решают проблему с ошибками первого рода, тогда предположив, что помеза представляет собой классический гаусовский поток интеграл описывающий хвост будет иметь вид:
Сигма0^2 – дисперсия шума. Интеграл Лапласа не берущийся. Имеет 2 подхода к решению:
Детектор для ортогональных сигналов(прямоугольной формы) примет вид Противоположные сигналы помехоустойчивее, чем ортогональных.
Известно, что использование двух позиционных сигналов по скорости ограничивается пределом Шеннона. В настоящее время есть 1 путь преодоления предела Шеннона: переход от двух позиционного сигнала к много позиционным сигналам. Для этого система передачи информации на передающей стороне получают устройства преобразования битового потока в дибитовый, трибитовый. ДСП – алгоритм бабочка Основа нейросетей.
|

 При всей его схожести с процессами гибели и размножения таковыми являются только процессы, имеющие 2е вершины.
При всей его схожести с процессами гибели и размножения таковыми являются только процессы, имеющие 2е вершины.