Потоки событий
Потоком событий в ТМО принято называть последовательность однородных событий следующих друг за другом в случайные моменты времени. События могут происходить через строго определенные интервалы времени, такой поток событий перестает быть случайным и получил название в ТМО регулярный поток. У регулярного потока интервалы времени между наступлениями событий имеют одиноковое значений. Как правило регулярные потоки существовать не могут, поэтому рассматривается еще несколько вариантов потоков. Поток может быть стационарным если число событий, возникающих на том или ином интервале времени зависит только от длины этого интервала времени, но не зависит от того, где этот интервал расположен на временной оси. Поток называется ординарным, если вероятность возниконвоения двух событий и более в один случайный момент времени пренебрежимо мала по сравнению с вероятностью возниконвения ровно одного события в случайный момент времени. Поток называется потоком с отсутствием последействия, если для любых двух непересекающихся отрезков времени число событий выпавших на один отрезок никоим образом не зависит от числа событий выпавших на другой отрезок. Особый класс потоков для которых одновременно выполняется все три этих свойства называется простейшим потоком или стационарным пуассоновским потоком, как правило стремятся все потоки свести к простейшим, потому что в этом случае описание функционирования системы становится простейшим. Для простейшего потока так же как в теории вероятностей имеется аналогия. Так в теории вероятностей определено, что если принимать во внимание все события, то общий закон распределения будет нормальным. ПО аналогии с математикой принято считать, что объединение достаточно большого числа потоков событий с разными характеристиками в целом приводят к простейшему потоку с интенсивностью
Если предположить, что речь идет о потоке отказов, то гарфически его можно изобразить:
В момент возникновения отказа являются случайными моментами, то интервал времени отказа будет равен
Тогда интенсивность отказов буте равна
Если после каждого отказа восстановление осуществлялось в течении интервала времени тау1, тау2, тау3, то среднее время восстановления будет равно
M – число событий попадающих на интервал Δ t. Например вероятность того, что на интервал Δ t не попадет ни одного события:
Вероятность того, что на некоторый интервал дельта t попадет хотя бы одно событие.
Известно, что для такой плотности вероятности распределения событий математическое ожидание
Вывод:
|

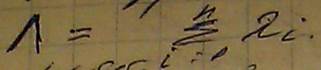

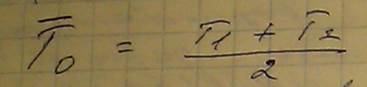

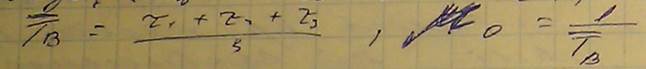 Если поток является простейшим, то для него в ТМО доказано, что число событий попадающих на некоторый интервал времени дельтаt подчиняется закону Пуассона, который записывают:
Если поток является простейшим, то для него в ТМО доказано, что число событий попадающих на некоторый интервал времени дельтаt подчиняется закону Пуассона, который записывают: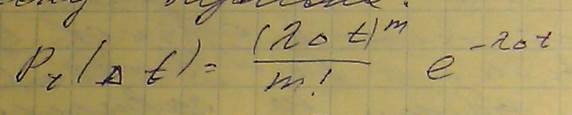
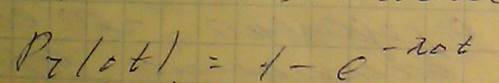

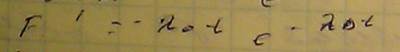 - плотность распределения
- плотность распределения




