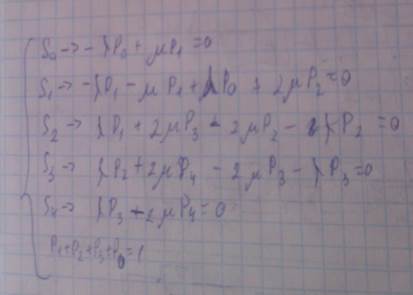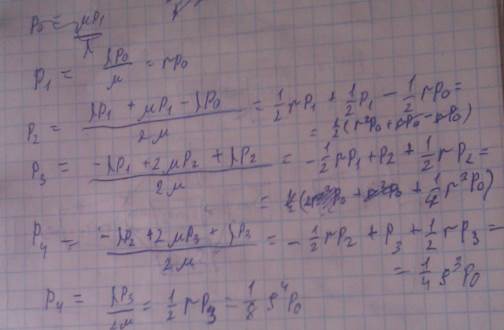Процесс гибели и размножения

Среди всех процессов используемых в теории массового обслуживания при принятии решений в том числе особое место занимают процессы гибели и размножения.

Для процессов гибели и размножения характерна эргодичность, т.е. эти процессы всегда имеют финальные, стационарные состояния. Этим финальным состоянием соответствуют финальные вероятности.

Финальные состояния наступают после окончания в системе переходных процессов и эти финальные вероятности не зависят от всякой хуйни начального состояния системы.

Эргодическими называются системы, которые за конечное число шагов могут всегда переходить из любого состояния в любое другое состояние, а для финальных вероятностей характерно выполнение условия нормировки, т.е. сумма финальных вероятностей всегда должна быть равна единице.

Одной из таких задач является задача анализа пропускной способности локальной сети, реализованной на основе коммутируемой технологии эзернет.

Предположим, что структура локальной сети представляет собой схему

Потоками кадров с любой другой рабочей станции и предположим так же что на входе каждого порта коммутатора имеется буферная память объемом на 2 кадра.

Требуется рассчитать основные хар-ки функционрирования такой системы. Из анализа системы она представляет собой систему массового обслуживания, где кадры поступающие на комутатор от рабочих станций являются заявками, т.е. рабочие станции создают потоки событий, а коммутатор образует канал обработки информации.

Предположим для простоты, что все потоки формируемые рабочими станциями являются простейшими. На коммутатор двух и более заявок одновременно и менее вероятно, чем вероятность поступления одной заявки.

С точки зрения теории массового обслуживания такую систему можно представить следующей схемой, имеется канал обработки информации

Если кадр от рабочей станции поступает в то время, когда и канал обработки и первое буфферное устройство, то такая заявка получает отказ и формируется поток отказа обработки.

Отметим, что в такой постановке отказы обработки возникают только по занятости канало и буфферных устройств.

Не рассматриваются проблемы связанные с аппаратными и программными средствами.

Предположим лямбда =10 кадр/c

Интенсивность обработки мю= 20 кадр/с

В системах, характеризуемых процессами гибели и размножения вводится понятие относительной интенсивности поступления заявок, ее обозначают РО=лямба/мю=10/20=0,5

В наличии ро по значению меньше 1 – первое основание для того, чтобы считать в данной системе могут быть финальные состояния. Для решения такой задачи составим

состояний и переходов системы:

S0 -отсутствие заявок на входе системы

Лямбда – переход в состояние S1

S1 – на вход системы поступила одна заявка на обслуживание. Канал обработки занят, а буферные устройства свободны.

Если в момент времени, когда в канале обработки продолжает обрабатываться первая заявка на вход системы поступает вторая заявка, тогда система с той же интенсивностью лямбда перейдет в состояние S2, в котором занятый канал обработки и занято одно буферное устройство. Если в момент времени, когда в канале обработки происходит обработка первого кадра на вход системы, то она переводит систему в S3

S3 – занят канал обработки, заняты первое и второе буферное устройство.

Вторая заявка из первого буферного устрйоства поступает в канал обработки, а вторая в первый, этот процес происходит с интенсивностью мю.

Такой процесс, у которого для каждого состояния имеется вход увеличивающий состояние и выход уменьшающий состояние называется процессом гибели, наоборот размножения

Из анализа графа следует, что такая система за конечное число шагов всегда может перейти из любого состояния в любое другое называют эргодической.

Для всех эргодических систем определяется принцип достаточности наличия финальных вероятностей, обозначим их Р0,Р1,Р2,Р3.

Когда говорят о наличии финальных вероятностей, то следовательно переходный процесс в такой системе стал стационарным и следовательно первая производная от этих вероятностей Р0(t),P(1)(t),P2(t),P3(t) будут равны 0 и правые части ур-я Колмогорова будут равны 0. Функционирование такой системы уже описывается не системой диф. Ур, и система не является задачей Коши, а системой обычных алгеброических уравнений, которые составляются по общему правилу, по которому составляются диф ур Колмогорова, только левые части равны 0.

 

Основные характеристики системы массовго обслуживания вычисляются в результате решения системы алегбраических уравнений Колмагорова. Система составляюется по графу состояний и переходов. В следствии того, что в данном случае рассматриваются финальные вероятности левые части уравнений (производные от вероятностей по времени) равны 0.

Уравнения составляются для каждого состояния отдельно причем исходящие ветви берутся со знаком минус. А входящие ветви со знаком +. Составим систему уравнений Колмагорова:

S0->-лямбда*P0+мю*P1=0

 

S1->-лямбда*Р1+лямбда*Р0+мю*Р2-мю*Р1=0

S1->-Р1*(лямбда+мю)+лямбда*Р0+мю*Р2=0

 

S2->-лямбда*Р2+лямбда*Р1+мю*Р3-мю*Р2=0

S2->-(лямбда+мю)*Р2+лямбда*Р1+мю*Р3=0

 

S3->лямбда*Р3-мю*Р3=0

Р0+Р1+Р2+Р3=1

ro=лямбда/мю

Решаем систему уравнений в следующем порядке:

1. Из первого уравнения выражаем р1 через р0 и получим Р1=rо*Р0 rо – относительная интенсивность поступления заявок
2. Из второго уравнения выразим Р2 через Р1 и Р0 Р2=rо^2*Р0
3. Из 3его Р3 через Р2, Р1 и Р0 Р3=rо^3*Р0
4. Из уравнения нормировки находим выражения для вычисления Р0

Р0=1-rо*Р0-rо^2*P0-rо^2*P0

P0=(1+ro+ro^2+ro^3)^(-1)

1. Выражения для вычисления финальных вероятностей рассчитывают их значения по заданным лямбда и мю. Р0=0,53 Р1=0,265 Р2=0,1325 Р3=0,06625
2. По полученным значениям финальных вероятностей вычисляют основные характеристики системы массового обслуживания:

- среднее число заявок в системе Lсист=ro/(1-ro)=1

- среднее время заявок в системе Тс чертой сист.=Lсист/лямбда=0,1с

- вероятность простоя системы Рпростоя=Р0=0,53

- среднее число заявок в очереди Lоч=ro^2/(1-ro)=0.5

- среднее время пребывания заявки в очереди Т с чертой оч.=Lоч/лямбда=0,05с

- вероятность отказа Ротк=Р3=0,07

- относительная пропускная способность - вероятность того, что заявка будет обслужена Q=1-(Pотк-Р3)=0,93

Абсолютная пропускная способность A=лямбда*Q=9.3

 

Многоканальная система массового обслуживания с ограниченной очередью

На практике значительная часть коммутационных систем строится так, что каналов обработки информации может быть не 1, а несколько, например N, на каждый канал обработки могут быть свои или общие буферные регистры. Требуется сформулировать формальное описание такой задачи, рассчитать значения финальных вероятностей и основные характеристики такой СМО. Приняв при этом, что число каналов N=2, а буферные регистры на оба канала являются общими и рассчитаны на m=2 кадра. Характеристики лямбда и мю принять 10 и 20 кадров в секунду соответственно.

По вербальному описанию задачи составим ее формальное представление, то есть модель задачи.

по данному формальному оформлению строим граф состояний и переходов для многоканальных СМО с отказами.

Естественно, что все эти задачи в настоящее время решены и получены общие формулы для вычисления основных характеристик систем массового обслуживания. Запишем их в виде таблицы

 

показатели	одноканальная СМО с огранич очередью	многоканальная смо с ограниченной очередью
предельная вероятность	Р0=(1-ro)/(1-ro^(n+2))H1=ro*P0 Pk=ro^k*P0