Преобразования случайных функций [1, 26, 27].
Системы преобразования случайных функций. Пусть имеется система преобразования сигналов с одним входом и с одним выходом. На вход поступает (подается) входная случайная функция X(t) - функция воздействия или возбуждения. С выхода снимается выходная функция Z(t) – отклик или выходная реакция системы. Система осуществляет преобразование X(t) Þ Z(t) и описывается определенным системным оператором трансформации Т - функцией, алгоритмом, набором правил преобразования входного сигнала в выходной. Функциональное обозначение операции преобразования: Z(t) = T[X(t)]. Символическое отображение операции преобразования: z(t) = h(t) * x(t-t), где h(t) - математическая функция импульсного отклика системы на единичное входное воздействие. Это выражение представляет собой краткую запись операции свертки, которой реализуется линейное преобразование. В интегральной форме: z(t) = Импульсный отклик определяет соответствующую частотную передаточную характеристику системы: h(t) ó H(w). Для неслучайных (детерминированных) входных сигналов соотношение между выходными и входными сигналами всегда однозначно задается системным оператором. В случае реализации на входе системы случайного входного процесса (случайного сигнала) тоже существует однозначное соответствие процессов на выходе и входе системы, однако при этом одновременно происходит изменение статистических характеристик выходного сигнала (математического ожидания, дисперсии, ковариационной функции и пр.). Линейные и нелинейные системысоставляют два основных класса систем обработки сигналов. Термин линейности означает, что система преобразования сигналов должна иметь произвольную, но в обязательном порядке линейную связь между входным сигналом (возбуждением) и выходным сигналом (откликом). В нелинейных системах связь между входным и выходным сигналом определяется произвольным нелинейным законом. Основные системные операции линейных систем, из которых могут быть сформированы любые линейные операторы преобразования, это операции скалярного умножения, сдвига и сложения сигналов: s(t) = c ´ a(t), s(t) = a(t-Dt), s(t) = a(t)+b(t). Для нелинейных систем выделим важный тип безинерционных операций нелинейной трансформации сигнала, результаты которой зависят только от его входных значений. К ним относятся, например, операции квадратирования и логарифмирования сигнала: y(t) = [s(t)]2, y(t) = log[s(t)]. Система считается линейной, если реакция системы на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия): T[a(t)+b(t)] = T[a(t)]+T[b(t)], T[c ´ a(t)]= c ´ T[a(t)]. Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных. Линейные системы могут быть неоднородными, если они осуществляют какое-либо линейное однородное преобразование с прибавлением (вычитанием) заданной функции, т.е. операцию вида Z(t) = T[X(t)] = To[X(t)] + f(t). Двухвходовая система описывается системным оператором Т, который связывает два входных воздействия, соответственно X(t) и Y(t), с выходной реакцией Z(t). Система считается линейной, если принципы аддитивности и однородности выполняются для обоих входов, т.е.: Z(t) = T[c×X(t), c×Y(y)] = c×T[X(t),Y(t)], Z(t) = T[X1(t)+X2(t), Y1(t)+Y2(t)] = T[X1(t),Y1(t)]+T[X2(t),Y2(t)]. Двухвходовая система может применяться, например, для суммирования двух случайных процессов с разными коэффициентами усиления их значений. При выполнении линейных преобразования над случайными сигналами обычно ставится задача определения характеристик распределения выходного распределения Z(t) по известным характеристикам входного распределения сигнала X(t). Математическое ожидание выходного сигнала: mz(t) = M{Z(t)} = M{T[X(t)]}. Из теории линейных систем: Линейный оператор можно выносить за знак математического ожидания. Отсюда следует: mz(t) = T[M{X(t)}] = T[mx(t)], (9.3.1) т.е. для определения функции математического ожидания выходного сигнала Z(t) достаточно выполнить преобразование тем же системным оператором функции математического ожидания входного сигнала X(t): mz(t) = h(t) * mx(t-t). (9.3.2) Корреляционная функция выходного сигнала: Rz(t1, t2) = M{Z(t1)Z(t2)}= M{T1[X(t1)] T2[X(t2)]}, где Т1 и Т2 - один и тот же оператор Т по переменным соответственно t1 и t2, что позволяет вынести его за знак математического ожидания, сохраняя переменные: Rz (t1, t2) = T1T2[M{X(t1)X(t2)}] =T1T2[Rx(t1,t2)], (9.3.3) т.е. при известной функции корреляции входного сигнала функция корреляции выходного сигнала находится двойным преобразованием тем же оператором по двум аргументам. При определении функции Rz(t) следует учесть порядок преобразования. Для произведения выходных сигналов z(t) и z(t+t) линейной системы можно записать: z(t)×z(t+t) = Если взять математические ожидания от обеих частей этого равенства, то, с учетом соотношения в подынтегральном выражении M{x(t-a) x(t+t-b)} = -Rx(t-a-t-t+b) = Rx(t+a-b), получим: Rz(t) = Таким образом, функция корреляции выходного сигнала равна функции корреляции входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом системы, что сохраняет четность корреляционной функции выходного сигнала. Аналогичное заключение действительно и для ковариационных функций. Заметим, что для свертки импульсных откликов, производя замену t-b = t, мы имеем равенство: h(t+a) * h(t-b) = h(t+a+b) * h(t) = h(t) * h(t+g) = Rh(t), где Rh(t) - функция корреляции импульсного отклика системы. Отсюда: Rz(t) = Rx(t) * Rh(t), (9.3.5) т.е. функция корреляции выходного сигнала равна свертке функции корреляции входного сигнала с функцией корреляции импульсного отклика системы. Это означает появление в случайном сигнале на выходе системы определенной корреляционной зависимости, вызванной инерционностью системы, причем радиус корреляции выходного сигнала обратно пропорционален верхней частоте, пропускаемой системой. Функции взаимной корреляции входного и выходного сигналов определяются аналогично: Rzx (t1, t2) = T1[Rx(t1, t2)], Rxz(t1, t2) = T2[Rx(t1, t2)]. (9.3.6) Для функции Rxz входного и выходного сигналов имеем:
Rxz(t) = т.е. функция взаимной корреляции входного и выходного сигналов равна свертке функции корреляции входного сигнала с функцией импульсного отклика системы. Другая взаимно корреляционная функция Ryx может быть получена из соотношения: Rzx(t) = Rxz(-t) º Rx(t) * h(t+a). (9.3.8) Отметим, что для статистически независимых случайных величин при одностороннем импульсном отклике h(t) = 0 при t<0 функция Rxz(t) также является односторонней и равна 0 при t<0, а функция Rzx соответственно равна 0 при t>0. Спектральные соотношения, которые характеризуют систему в целом по отношению к преобразованию случайных сигналов, это соотношения спектральных плотностей случайных сигналов (спектров мощности) на входе и выходе. Применяя преобразование Фурье к левой и правой части выражения (9.3.5), для спектра мощности выходного сигнала получаем: Sz(f) = Sx(f) |H(f)|2. (9.3.9) Спектр мощности случайного сигнала на выходе системы равен спектру мощности входного сигнала, умноженному на квадрат модуля частотной характеристики фильтра. С учетом четности ковариационных функций спектр мощности выходного сигнала также является четной действительной функцией и содержит только амплитудную характеристику системы. Аналогично, для взаимного спектра мощности сигналов на основе выражений (9.3.7-8) имеем: Sxz(f) = Sx(f) H(f). (9.3.10) Szx(f) = Sx(f) H(-f). (9.3.10') Взаимный спектр сигналов при одностороннем импульсном отклике является комплексным, и содержит как амплитудную, так и фазовую характеристику системы. Отметим, что с использованием выражения (9.3.10) можно производить определение частотной характеристики и импульсного отклика системы: H(f) = Sxz/Sx Û h(t). Дисперсия выходного сигнала может быть определена с использованием формул (9.3.4, 9) по функциям ковариации: sz 2 = Kz(0) = Если сигнал нецентрированный и значение дисперсии входного сигнала неизвестно, то по аналогичным формулам вычисляется сначала средний квадрат выходного сигнала или так называемая средняя мощность сигнала:
Средняя мощность выходного сигнала равна средней мощности входного сигнала, умноженной на квадрат площади импульсной реакции системы (для цифровых систем - сумму квадратов коэффициентов импульсного отклика). Для центрированных случайных сигналов средняя мощность равна дисперсии сигналов. Для нецентрированных выходных сигналов: sz 2 = Функция когерентности дает оценку точности принятой линейной модели системы. Когерентность входного и выходного сигналов системы оценивается по формуле: gxz2(f) = |Sxz(f)|2/[Sx(f)×Sz(f)]. (9.3.14) Если функции Sx(f) и Sz(f) отличны от нуля и не содержат дельта-функций, то для всех f значения функции когерентности заключены в интервале: 0 £ gxz2(f) £ 1. Для исключения дельта-функций на нулевой частоте определение функции когерентности производится по центрированным сигналам. Для линейных систем с постоянными параметрами функция когерентности равна 1, в чем нетрудно убедиться, если в формулу (9.3.14) подставить выражения Sxz и Sz, определенные через Sx в формулах (9.3.9-10). Для совершенно не связанных сигналов функция когерентности равна нулю. Промежуточные между 0 и 1 значения могут соответствовать трем ситуациям: 1. Система осуществляет преобразование x(t) Þ z(t), но в измерениях этих сигналов или одного из них присутствует внешний шум. Так, например, в сигналах, зарегистрированных с ограничением по разрядности, появляется шум квантования (округления значений). 2. Система не является строго линейной. Это может наблюдаться, например, при определенном ограничении по разрядности вычислений в цифровых системах, при накоплении ошибки в рекурсивных системах и т.п. 3. Выходной сигнал z(t) помимо x(t) зависит еще от каких-то входных или внутренних системных процессов. Величина 1-gxz2(f) задает долю среднего квадрата сигнала z(t) на частоте f, не связанную с сигналом x(t). Аналогично можно вычислить функцию когерентности двух реализаций x(t) и y(t). Значения функции будут указывать на степень линейной зависимости одной реализации от другой, хотя это и не означает обязательности наличия какой-либо причинно-следственной связи между реализациями. Функция когерентности gxy сохраняется при точных однотипных линейных преобразованиях функций x(t) и y(t), что позволяет производить ее определение не измеряя самих величин x(t) и y(t). Использование функций когерентности в практических методах анализа случайных данных подробно рассмотрено в работе /л4/. Преобразования случайных функций. Сложение случайных функций. При сложении случайных функций, в общем случае, с произвольными постоянными коэффициентами а и b, и образовании случайной функции суммы Z(t) = a×X(t) + b×Y(t) функция математического ожидания процесса Z(t): mz(t)= M{Z(t)}= M{aX(t)+bY(t)}= a×M{X(t)}+b×M{Y(t)}= a×mx(t)+b×my(t). (9.3.15) Корреляционная функция суммы вычисляется аналогично и равна: Rz(t1, t2) = M{Z(t1)×Z(t2)}= M{[aX(t1)+bY(t1)][aX(t2)+bY(t2)]} = = M{a2X(t1)X(t2)+b2Y(t1)Y(t2)+×ab[X(t1)Y(t2)+Y(t1)X(t2)]} = = a2Rx(t1, t2)+b2Ry(t1, t2)+ab×[Rxy(t1, t2)+Ryx(t1, t2)]. (9.2.16) Для некоррелированных функций X(t) и Y(t) функции взаимной корреляции Rxy и Ryx обнуляются. Аналогичную форму записи имеют и ковариационные функции (как частный случай корреляционных функций при центрировании случайных процессов). Выражения легко обобщаются на сумму любого числа случайных функций. В частности, для корреляционной функции стационарной случайной функции Z(t) = Rz(t) = При сложении случайной функции X(t) с неслучайной функцией y(t) математическое ожидание и корреляционная функция суммы Z(t)=X(t)+y(t) равны: mz(t) = mx(t) + y(t), Rz(t1, t2) = Rx(t1, t2). (9.3.17) При сложении случайной функции X(t) с некоррелированной случайной величиной Y математическое ожидание и корреляционная функция суммы Z(t)=X(t)+Y: mz(t) = mx(t) + my, Rz(t1, t2) = Rx(t1, t2) + Dy. (9.3.18) Произведение случайной и неслучайной функций X(t) и f(t).Математическое ожидание и корреляционная функция выходного сигнала: mz(t) = M{Z(t)} = M{f(t)×X(t)} = f(t)×M{X(t)} = f(t)×mx(t). (9.3.19) Rz(t1, t2)=M{f(t1)X(t1) f(t2)X(t2)}= f(t1)f(t2)M{X(t1)X(t2)}= = f(t1)f(t2)×Rx(t1, t2). (9.3.20) Если f(t) = const = C и Z(t) = C×X(t), то соответственно имеем: mz(t) = С×mx(t), Rz(t1, t2) = С2×Rx(t1, t2). (9.3.21) Производная от случайной функции Z(t) = dX(t)/dt. Если функция X(t) является непрерывной и дифференцируемой, то математическое ожидание производной: mz(t) = M{Z(t)} = M{dX(t)/dt} = d(M{X(t)})/dt = dmx(t)/dt, (9.3.22) т.е. математическое ожидание производной от случайной функции равно производной от ее математического ожидания. Для корреляционной функции имеем: Rz(t1,t2) = M{(dX(t1)/dt1)(dX(t2)/dt2)}= т.е. корреляционная функция производной случайной функции равна второй смешанной частной производной от корреляционной функции исходной случайной функции. Интеграл от случайной функции Z(t) = mz(t) = M{Z(t)} = M{ т.е. математическое ожидание интеграла от случайной функции равно интегралу от ее математического ожидания. Для корреляционной функции имеем: Rz(t1, t2) = M{ = т.е. корреляционная функция интеграла от случайной функции равна двойному интегралу от корреляционной функции исходной случайной функции. Преобразования стационарных случайных функций выполняются по вышеприведенным формулам, и приводят к следующим результатам (вместо корреляционных функций приводятся ковариационные функции, которые обычно используются на практике). Математическое ожидание выходного сигнала Z(t) входной стационарной случайной функции X(t) по (9.3.2): mz = h(t) * mx = mx Отсюда следует, что математическое ожидание выходных сигналов системы равно математическому ожиданию входных сигналов, умноженному на площадь (или сумму коэффициентов) импульсного отклика системы, т.е. на коэффициент усиления системой постоянной составляющей. Если система не пропускает постоянную составляющую сигналов (площадь или сумма коэффициентов импульсного отклика системы равна нулю), то случайный выходной сигнал всегда будет иметь нулевое математическое ожидание. Сумма двух стационарных случайных функций X(t) и Y(t) дает стационарную случайную функцию Z(t), при этом: mz = mx + my, Dz = Dx + Dy + 2Kxy(0). (9.3.27) Kz(t1, t2) = Kz(t) = Kx(t) + Ky(t) + Kxy(t) + Kyx(t). (9.3.28) Сумма стационарной случайной и неслучайной функций X(t) и y(t) нестационарна по математическому ожиданию: mz(t) = mx + y(t), Kz(t) = Kx(t). (9.3.29) Произведение стационарной случайной и неслучайной функций X(t) и y(t) - нестационарная случайная функция, так как: mz(t) = y(t)×mx, Dz(t) = y2(t)×Dx. (9.3.30) Kz(t, t) = y(t)y(t+t)Kx(t). (9.3.31) Производная от стационарной случайной функции - стационарная случайная функция с математическим ожиданием mz = 0 и ковариационными функциями: Kz(t1, t2) = Kzx(t) = d(Kx(t))/dt, Kxz(t) = -d(Kx(t))/dt. (9.3.33) Из выражения (9.3.32) следует также, что для дифференцируемости X(t) необходимо, чтобы ее ковариационная функция была дважды дифференцируемой по t. Интеграл от стационарной случайной функции - нестационарная случайная функция с математическим ожиданием mz(t) = Kz(t1, t2) =
|

 h(t)×x(t-t) dt.
h(t)×x(t-t) dt.
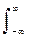 Sx(f) |H(f)|2 df º Kx(0)
Sx(f) |H(f)|2 df º Kx(0) 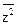 =
=  = Rz(0) º
= Rz(0) º 
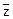 2 º (
2 º ( 2)
2)  anXn(t) при t2-t1 = t имеем:
anXn(t) при t2-t1 = t имеем:
 M{X(t1)X(t2)}=
M{X(t1)X(t2)}=  X(v)dv.
X(v)dv. h(t) dt, (9.3.26)
h(t) dt, (9.3.26) Kx(t) = Kz(t). (9.3.32)
Kx(t) = Kz(t). (9.3.32)
 Kx(u1-u2) du1 du2. (9.3.34)
Kx(u1-u2) du1 du2. (9.3.34)


