Каноническое уравнение гиперболы.
Определение 1. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Составим уравнение гиперболы с фокусами в данных точках F1 и F2. Для этого выберем прямоугольную систему координат так, чтобы ось Ох проходила через фокусы, а начало координат делило отрезок F1F2 пополам (рис. 1). Обозначив F1F2 = 2с, получим F1 (с; 0) и F2 (–с; 0). Пусть М (х; у) – произвольная точка гиперболы.
Рис. 1
Определение 2. Расстояния r1 = F1M и r2 = F2M называются фокальными радиусами точки М. Согласно определению гиперболы | r1—r2 | =2a , (1) где 2а – величина постоянная и 2а < 2с, т.е. а < с. Подставив
вравенство (1), получим уравнение гиперболы
Уравнение (2) можно привести к более простому виду; для этого преобразуем его следующим образом:
т.е.
Так как а < с, то с2 – а2 > 0. Положим с2 – а2 = b2 ;(3) тогда последнее равенство принимает вид b2x2 – a2y2 = a2b2, или
(4)
Как и в случае эллипса, можно показать, что справедливо и обратное: если координаты точки М (х; у) удовлетворяют уравнению (4), то она принадлежит гиперболе. Определение 3. Уравнение (4) называется каноническим уравнением гиперболы.
|


 и
и 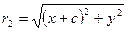
 . (2)
. (2) ,
, ,
,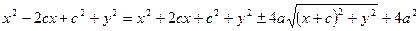 ,
, ,
,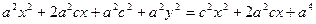 ,
, .
.



