Каноническое уравнение эллипса.
Определение 1. Э лл ипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, бóльшая, чем расстояние между фокусами.
Рис. 1
Составим уравнение эллипса с фокусами в данных точках F1 и F2. Для этого выберем прямоугольную систему координат так, чтобы ось Ох проходила через фокусы, а начало координат делило отрезок F1F2 пополам (рис.1). Обозначив F1F2=2c, получим F1 (c; 0) и F2 (–с; 0). Пусть М (х; у) – произвольная точка эллипса. Определение 2. Расстояния r1=F1M и r2=F2M называются фокальными радиусами точки М. Положим
тогда согласно определению эллипса 2а – величина постоянная, причем 2а>2с, т.е. а>с. По формуле расстояния между двумя точками находим
Подставив найденные значения r1 и r2 в равенство (1), получим уравнение эллипса
Преобразуем уравнение (3) следующим образом:
т. е.
Так как а > с, то а2–с2>0. Положим
тогда последнее уравнение примет вид
или (5)
Так как координаты х и у любой точки М эллипса удовлетворяют уравнению (3), то они удовлетворяют и уравнению (5). Покажем, что справедливо и обратное: если координаты точки М(х; у) удовлетворяют уравнению (5), то она принадлежит эллипсу. Пусть М (х; у) – произвольная точка, координаты которой удовлетворяют уравнению (5). Так как из (5) следует
то Подставив (6) в соотношения (2) и проведя необходимые упрощения, получим
Но так как а > с > 0 и
откуда
и, следовательно, Определение 3. Уравнение (5) называется каноническим уравнением эллипса.
|


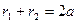 ; (1)
; (1) и
и 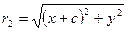 . (2)
. (2) (3)
(3)





 (4)
(4)

 (6)
(6) откуда
откуда 
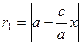 и
и 
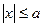 , то
, то и
и 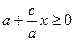 ,
, и
и  (7)
(7)


