Каноническое уравнение параболы.
Определение 1. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, не проходящей через данную точку и называемой директрисой. Составим уравнение параболы с фокусом в данной точке F и директрисой которой является прямая d, не проходящая через F. Выберем прямоугольную систему координат следующим образом: ось Ох проведем через фокус F перпендикулярно директрисе d в направлении от d к F, а начало координат О расположим посередине между фокусом и директрисой (рис. 1).
Рис. 1 Определение 2. Расстояние от фокуса F до директрисы d называется параметром параболы и обозначается через р (р > 0). Из рис. 1 видно, что p = FK, следовательно, фокус имеет координаты F (р/2; 0), а уравнение директрисы имеет вид х = – р/2, или
Пусть М(х; у) – произвольная точка параболы. Соединим точку М с F ипроведем MN а по формуле расстояния между двумя точками Согласно определению параболы, MF = MN, (1) следовательно, Уравнение (2) является искомым уравнением параболы. Для упрощения уравнения (2) преобразуем его следующим образом:
(3)
Координаты х и у точки М параболы удовлетворяют условию (1), а следовательно, и уравнению (3). Определение 3. Уравнение (3) называется каноническим уравнением параболы. 2. Исследование формы параболы по ее уравнению. Определим форму параболы по ее каноническому уравнению (3). 1) Координаты точки О (0; 0) удовлетворяют уравнению (3), следовательно, парабола, определяемая этим уравнением, проходит через начало координат. 2) Так как в уравнение (3) переменная у входит только в четной степени, то парабола у2 = 2рх симметрична относительно оси абсцисс.
Рис. 2.
3) Так как р > 0, то из (3) следует х ≥ 0. Следовательно, парабола у2 = 2рх расположена справа от оси Оу. 4) При возрастании абсциссы х от 0 до +∞ ордината у изменяется от 0 до ± ∞, т.е. точки параболы неограниченно удаляются как от оси Ох, так и от оси Оу. Парабола у2 = 2рх имеет форму, изображенную на рис. 2. Определение 4. Ось Ох называется осью симметрии параболы. Точка О (0; 0) пересечения параболы с осью симметрии называется вершиной параболы. Отрезок FM называется фокальным радиусом точки М. Замечание. Для составления уравнения параболы вида у2 = 2рх мы специальным образом выбрали прямоугольную систему координат (см. п. 1). Если же систему координат выбрать другим образом, то и уравнение параболы будет иметь иной вид.
б в
Рис. 3
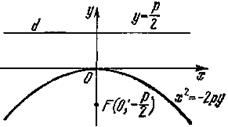
Так, например, если направить ось Ох от фокуса к директрисе (рис. 3, а), то уравнение параболы примет вид у2 = –2рх. (4) Фокус такой параболы имеет координаты F(–р/2; 0), а директриса d задана уравнением х = р/2. Если ось Оу проведем через фокус F перпендикулярно к директрисе d в направлении от d к F, а начало координат О расположим посередине между фокусом и директрисой (рис. 3, б), то уравнение параболы пример вид х2 = 2ру. (5) Фокус такой параболы имеет координаты F (0; р/2), а директриса d задана уравнением у=–р/2. Если ось Оу проведем через фокус F перпендикулярно к директрисе d в направлении от F к d (рис. 3, в), то уравнение параболы примет вид х2 = –2ру (6) Координаты ее фокуса будут F (0; –р/2), а уравнением директрисы d будет у = р/2. Об уравнения (4), (5), (6) говорят, что они имеют простейший вид.
Рис. 4
3. Параллельный перенос параболы. Пусть дана парабола с вершиной в точке О' (а; b), ось симметрии которой параллельна оси Оу, а ветви направлены вверх (рис. 4). Требуется составить уравнение параболы.
Определение 5. Уравнение (9) называется уравнением параболы со смещенной вершиной. Преобразуем это уравнение следующим образом:
Положив
будем иметь
Нетрудно показать, что для любых А, В, С график квадратного трехчлена (10) представляет собой параболу в смысле определения 1. Уравнение параболы вида (10) изучалось в школьном курсе алгебре.
|



 d. Непосредственно из рис. 1 видно, что
d. Непосредственно из рис. 1 видно, что 

 (2)
(2)
 т.е.,
т.е.,
 а
а

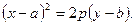 (9)
(9)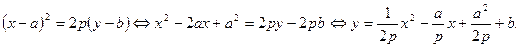

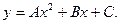 (10)
(10)


