Исследование формы гиперболы по ее уравнению.
Определим форму гиперболы по ее каноническому уравнению (4). 1) Координаты точки О (0; 0) не удовлетворяют уравнению (4), поэтому гипербола, определяемая этим уравнением, не проходит через начало координат. 2) Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (4) у = 0, найдем х = ± а. Следовательно, гипербола пересекает ось Ох в точках A1 (a; 0) и А2 (–а; 0). Положив в уравнении (4) х = 0, получим у2 = – b2, а это означает, что система
не имеет действительных решений. Следовательно, гипербола не пересекает ось Оу. 3) Так как в уравнение (4) переменные х и у входят только в четных степенях, то гипербола симметрична относительно координатных осей, а следовательно, и относительно начала координат. 4) Определим область изменения переменных х и у;для этого из уравнения (4) находим
Из (5) следует, что |х| ≥ а, т.е. х ≥ а или х ≤ –а; из (6) следует, что у – любое действительное число. Таким образом, все точки гиперболы расположены слева oт прямой х = – а и справа от прямой х = а. 5) Из (5) следует также, что у → ± ∞; при х → + ∞;. у → ± ∞; при х → – ∞;. Это означает, что гипербола состоит из двух ветвей, одна из которых расположена справа от прямой х = а (правая ветвь гиперболы), а другая – слева от прямой х = – а (левая ветвь гиперболы).
Рис. 2
Гипербола имеет форму, изображенную на рис. 2. Определение 4. Точки А1 (а; 0) и А2 (а; 0) пересечения гиперболы с осью Ох называются вершинами гиперболы. Отрезок A1A2 (A1A2=2a),соединяющий вершины гиперболы, называется действительной осью. Отрезок B1B2 (B1B2=2b), соединяющий точки B1 (0; b) и В2 (0; – b), называется мнимой осью. Число а называется действительной полуосью, число b – мнимой полуосью. Оси А1А2 и В1В2 являются осями симметрии гиперболы. Точка О пересечения осей симметрии называется центром гиперболы. У гиперболы (4) фокусы F1 и F2 всегда находятся на действительной оси. Можно показать (так же, как и в случае эллипса), что фокальные радиусы для точки М (х; у), расположенной на правой ветви гиперболы, вычисляются по формулам
а для точки М (х; у), расположенной на левой ветви, – по формулам
|


 , (5)
, (5) . (6)
. (6)
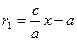 и
и  , (7)
, (7) и
и 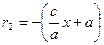 . (8)
. (8)


