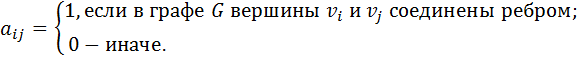Понятие связности, смежности и инцидентности

Если в графе любые две вершины можно соединить цепью, то граф называется связным. В противном случае он несвязный.

Связный граф, не содержащий циклов, называется деревом. Несвязный граф распадается на непересекающиеся максимальные связные компоненты (связные подграфы).

Вершины v_i, v_{i+ 1}, соединенные между собой ребром (дугой), называются смежными. Таким образом, смежность это отношение между вершинами.

С другой стороны, вершины v_i, v_{i+ 1} инцидентны ребру (дуги), которым они связаны.

Таким образом, инцидентность характеризует отношение между ребрами и вершинами. Ребро (дуга) инцидентно каждой вершине, которую оно соединяет. В результате можно сделать вывод, что граф задает два основных отношения: смежности и инцидентности. Степень вершины графа – число ребер, инцидентных ей. Если степень вершины графа равна 1, то она называется висячей. Если степень вершины графа равна 0, то она называется изолированной.

Пусть дан граф G с вершинами v ₁,…, v _n и ребрами х ₁,…, х_m.

Матрица смежности графа G – это квадратная матрица А(G) размера n x n (n – число вершин) с элементами

Матрица смежности графа G обладает свойством симметрии. Она показывает, существует ли путь длины 1 из вершины v _i в вершину v _j. Также можно получить информацию о путях большей длины. Для этого необходимо возвести матрицу смежности в нужную степень. m – степень матрицы смежности А^m, заполненная числами а_ij^(m), показывает число путей длины m из i вершины в j.

Дан орграф D с вершинами v ₁,…, v _n и дугами х ₁,…, х_m. Матрица смежности орграфа D – это квадратная матрица А(D) размера n x n (n – число вершин) с элементами

Матрица смежности орграфа D свойством симметрии не обладает.

Матрица инцидентности орграфа D – это матрица В(D) размера n x m (n – число вершин, m – число дуг) с элементами