Задача 1. Задан граф.
v 7 
|
v 5 
|
v 6 
|
v 8 
|
Найти кратчайший путь из вершины v1 в вершину v8.
Решение. Используя алгоритм задачи о нахождении кратчайшего пути из v1 в v8 в смысле наименьшего количества ребер, получим:
1. Вершине v1 припишем индекс 0.
2. Всем вершинам, смежным с v1 (v2 и v3), припишем индекс 1.
3. Всем вершинам, смежным v2 и v3 и не имеющим индекса (v5,v4,v6,v7), припишем индекс 2.
4. Всем вершинам, смежным с вершинами (v4,v5,v6,v7) и не имеющим индекса v8, припишем индекс 3.
Таким образом, вершина v8 получила индекс 3, а значит, длина кратчайшего пути из v1 в v8 равна 3. Построим этот путь или пути, если их несколько.
5. Среди вершин, смежных с v8, найдем вершины с индексом 3-1=2. Таких вершин три: v6,v7, v4.
6. Среди вершин, смежных с v4,v6,v7, найдем вершины с индексом 1. Таких вершин две: v2 и v3.
7. Среди вершин, смежных с v2 и v3, найдем вершины с индексом 0. Такая вершина одна и это v1.
Таким образом, было получено три кратчайших пути длины 3. Перечислим их: 1) v1,v2,v6,v8; 2) v1,v3,v7,v8; 3) v1,v3,v4,v8.
v 7 (2) 
|
v 5 (2) 
|
v 6 (2) 
|
v 8 (3) 
|
Задача 2. Задан орграф.
Найти кратчайший путь из вершины v1 в вершину v6 в смысле суммы весов дуг.
Решение. Используя алгоритм решения задачи о нахождении кратчайшего пути в смысле суммы весов дуг, получим:
1. Вершине v1 присвоим индекс 0, а всем остальным +¥.
2. Переберем вершины орграфа, смежные с вершиной v1 и имеющие дугу из v1 в эту же вершину. Вершине v4 присвоим индекс 0+2=2, так как 2<+¥. Вершине v3 присвоим индекс min {0+1, 2+2}=1, так как 1<+¥. Вершине v2 присвоим индекс min{0+1, 2+5}=2, так как 1<+¥.
3. Аналогично проведем рассуждения для вершин орграфа, смежных с вершинами v2,v3,v4. Так как в вершину v5 ведет две дуги, то присвоим ей индекс min{1+4, 2+3}=5<+¥. Вершине v7 присвоим индекс min{2+5, 1+3}=4<+¥.
4. Вершине v6 присвоим индекс min{5+2, 2+6, 4+1}=4+1=5. Таким образом, кратчайший путь из вершины v1 в v6 в смысле суммы весов дуг равен 5.
Построим этот путь.
5. Среди вершин, смежных с вершиной v6, найдем вершину С, для которой выполняется равенство 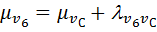 . Такой вершиной является v7, так как
. Такой вершиной является v7, так как  или 4+1=5.
или 4+1=5.
6. Среди вершин, смежных с вершиной v7, найдем вершину Д, для которой выполняется равенство  . Такой вершиной является v3, так как
. Такой вершиной является v3, так как 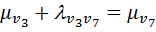 или 1+3.
или 1+3.
7. Среди вершин, смежных с вершиной v3, найдем такую вершину Е, для которой выполняется равенство  . Такая вершина одна и это v1.
. Такая вершина одна и это v1.
Таким образом, мы вернулись из вершины v6 в вершину v1.
Запишем кратчайший путь из v1 в v6: v1 v3 v7 v6.

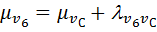 . Такой вершиной является v7, так как
. Такой вершиной является v7, так как  или 4+1=5.
или 4+1=5. . Такой вершиной является v3, так как
. Такой вершиной является v3, так как 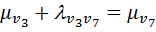 или 1+3.
или 1+3. . Такая вершина одна и это v1.
. Такая вершина одна и это v1.


