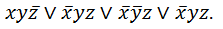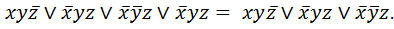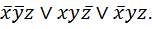ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Задача 1.Доказать, что булева функция (x®y)®((y®z)®(( ®z)) является тождественно истиной.
Задача 1. Доказать, что булева функция (x®y)®((y®z)®(( Решение.
Так как функция принимает значение 1 на всех наборах переменных, то по определению она является тождественно-истинной. Задача 2. Преобразовать в СДНФ булеву функцию, заданную формулой (х Þ у)(z+x). Решение. Действуем по стандартному алгоритму: 1. Добьемся, чтобы в формуле остались только дизъюнкции, конъюнкции и отрицания аргументов: (х Þ у)(z+x)= 2. Добьемся, чтобы конъюнкции выполнялись раньше дизъюнкций (раскроем скобки): 3. Делаем все элементарные конъюнкции правильными: 4. Делаем все элементарные конъюнкции полными: 5. Ликвидируем одинаковые элементарные конъюнкции: Задача 3. Рассмотрим получение СДНФ с помощью таблицы истинности на предыдущем примере
Решение. В последней колонки таблицы выбираем функции со значение 1. По исходным наборам, с учетом алгоритма записываем СДНФ:
|

 ®z)) является тождественно истиной.
®z)) является тождественно истиной.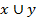

 y)
y) 
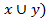 ®z))
®z))
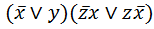 .
.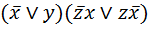 =
= 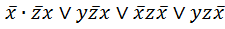 .
. .
. =
=