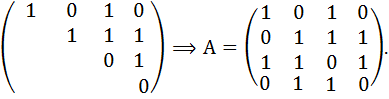ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Задача 1.Найти код Харари графа.
Задача 1. Найти код Харари графа.
Решение. Занумеруем вершины графа, выпишем матрицу смежности и ее верхний треугольник.
Легко увидеть, что данная нумерация вершин является канонической, так как, сменив нумерацию вершин, получим числа меньше числа 984. Следовательно, кодом Харари данного графа является число 984. Задача 2. Восстановить и нарисовать граф по числу 698 как по ходу Харари. Проверить, действительно ли нумерация вершин каноническая (т.е. является ли число кодом Харари). Решение. Переведем число 698 в двоичную форму, для чего будем делить его на 2, записывая справа от черты остатки от деления, а слева на следующей строке частные. 698|0 349|1 174|0 87|1 43|1 21|1 10|0 5|1 2|0 1| Записываем число, начиная с последнего частного и далее все остатки снизу вверх: 1010111010. Код Харари должен быть треугольным числом, т.е. иметь длину 1,3,6,10,15,21 и т.д., если длина не совпадает ни с одним из этих чисел, то добавляем слева необходимое количество нулей. Для числа 698 этого делать не нужно, так как треугольное число равно 10. Разбиваем число на разряды: 1010-111-01-0, выписываем эти числа в верхний треугольник матрицы, затем восстанавливаем всю матрицу, записывая ее строки по столбцам:
Восстановим по этой матрице граф с четырьмя вершинами
Заметим, что нумерация вершин не является канонической. Перенумеруем вершины.
Запишем матрицу смежности для получившегося графа
верхний треугольник = 11100110012=92110. 921>698, значит, число 698 кодом Харари не является.
|

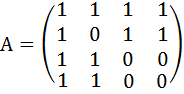 , верхний треугольник = 1111 011 0002=98410.
, верхний треугольник = 1111 011 0002=98410.