ТЕМА 3. БУЛЕВЫ ФУНКЦИИ
Булевой функцией y=f(x 1, x 2,…, x n) от n переменных x 1, x 2,…, x n называется любая функция, в которой аргументы и функция могут принимать значение либо 0, либо 1, т.е. булева функция это правило, по которому по произвольному набору нулей и единиц (x 1, x 2,…, x n) ставится в соответствие значение 0 или 1. Вектором значений булевой функции у = f(x 1, x 2,…, x n) называется упорядоченный набор всех значений функции f, при котором значения упорядочены по лексикографическому порядку. Среди булевых функций особо выделяются так называемые элементарные булевы функции, посредством которых можно описать любую булеву функцию от любого числа переменных. 1. Булева функция f(x 1, x 2,…, x n), принимающая значение 1 на всех наборах нулей и единиц, называется константой 1, или тождественной единицей. Обозначение: 1. 2. Булева функция f(x 1, x 2,…, x n), принимающая значение 0 на всех наборах нулей и единиц, называется константой 0, или тождественным нулем. Обозначение: 0. 3. Отрицанием называется булева функция одной переменной, которая определяется следующей таблицей истинности
Обозначения: Ø х, 4. Конъюнкцией называется булева функция двух переменных, которая определяется следующей таблицей истинности
Другие названия: логическое умножение (произведение); логическое «и». Обозначения: х × у, х Ù у, min(x,y). Запись может читаться так: «икс и игрек» или «икс умножить на игрек». 5. Дизъюнкцией называется булева функция двух переменных, которая определяется следующей таблицей истинности
Другие названия: логическое сложение (сумма); логическое «или». Обозначение: хÚу, max(x,y). Запись хÚу может читаться так: «икс или игрек» или «сумма икс и игрек». 6. Импликацией называется булева функция двух переменных, которая определяется следующей таблицей истинности
Другое название: логическое следование. Обозначения: х®у, хÞу, хÉу. Запись х®у может читаться так: из икс следует игрек». 7. Эквивалентностью называется булева функция двух переменных, которая определяется следующей таблицей истинности
Обозначения: х ~ у, х «у, х º у. Запись х ~ у может читаться так: «икс эквивалентно игрек» или «икс равносильно игрек». 8. Суммой по модулю_2 называется булева функция двух переменных, которая определяется следующей таблицей истинности
Другое название: антиэквивалентность. Обозначения: х Å у, х+у. Запись х Å у может читаться так: «икс плюс игрек». 9. Штрих Шерифа это булева функция двух переменных, которая определяется следующей таблицей истинности
Другое название: отрицание конъюнкции, логическое «не-и». Обозначение: х | у. Запись х | у может читаться так: «не икс или не игрек», «икс и игрек несовместны», «икс штрих Шеффера игрек». 10. Стрелка Пирса это булева функция двух переменных, которая определяется следующей таблицей истинности
Другое название: отрицание дизъюнкции, логическое £ не - или ³. Обозначение: х ¯ у. Все логические операции можно выразить через три логические операции (конъюнкция, дизъюнкция, отрицание).
Применение логических операций и функций определяются скобками. Если скобок нет, то логические операции применяются в следующей последовательности: отрицание, дизъюнкция, конъюнкция, импликация, эквиваленция. Определение. Две функции f 1 (x 1, …, x n) и f 2 (x 2, …, x n) называются равносильными, если они принимают одинаковое значение на одних и тех же наборах переменных. Функция от f 1 (x 1, …, x n) называется тождественно-истинной, если она принимает значения 1 на всех наборах своих переменных. Функция f 1 (x 1, …, x n) называется тождественно-ложной если она принимает значение 0 на всех своих наборах переменных. Рассмотрим 3 основные группы равносильности. 1. Основные равносильности · · · x* 1º x; · · x* 0º0; · · x * · · · · 2. Равносильности, выражающие одни логические операции другими · · · · · · · 3. Равносильности, выражающие основные законы алгебры и логики · · · · · · Для того чтобы сравнить две булевых функции, удобно привести их к некоторому стандартному виду. §1. Совершенная дизъюнктивная нормальная форма (СДНФ)
Пусть рассматривается булева функция от n переменных x 1, x 2,…, x n. Выражение Дизъюнкция нескольких ЭК называется дизъюнктивной нормальной формой (ДНФ). ЭК называется правильной, если ни одна переменная в ней не повторяется, и полной, если в ней участвуют все n переменных. Если в ДНФ все ЭК правильны и полны, то ДНФ называют совершенной (СДНФ). Справедлива следующая теорема: всякую булеву функцию можно представить в виде СДНФ и притом единственным образом. Алгоритм преобразования формулы в СДНФ: 1. Добьемся, чтобы в формуле остались только дизъюнкция, конъюнкция и отрицание над переменной:
2. Раскроем скобки и получим ДНФ. 3. Сделаем все ЭК правильными ( 4. Сделаем все ЭК полными (если ЭК не содержит переменную х, то умножим ее на 1= х 5. Вернемся к шагу 2. Через конечное число шагов получим СДНФ. В ней могут оказаться несколько одинаковых ЭК. Из таких ЭК составляем одну, согласно тождеству Для того, чтобы получить СДНФ с помощью таблицы истинности, необходимо: 1. Записать таблицу истинности. 2. В последнем столбце таблицы истинности выбрать 1. 3. В исходном наборе, соответствующем 1 последнего столбца таблицы, запишем 0 отрицанием переменной, а 1 самой переменной. 4. Записываем СДНФ булевой функции.
|

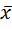 . Запись Ø х читается «не икс» или «отрицание икс».
. Запись Ø х читается «не икс» или «отрицание икс».



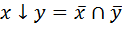
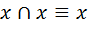 ;
; ;
; ;
;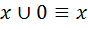 ;
; ;
;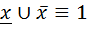 ;
; (закон двойного отрицания);
(закон двойного отрицания); (закон поглощения);
(закон поглощения); (закон поглощения).
(закон поглощения). ;
; ;
; ;
;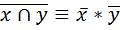 ;
; ;
;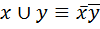 ;
; .
.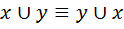 ;
;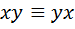 ;
; ;
; ;
; ;
; .
.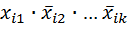 (отрицание на любых местах) называют элементарной конъюнкцией (ЭК).
(отрицание на любых местах) называют элементарной конъюнкцией (ЭК).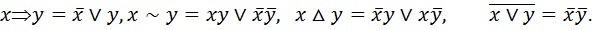
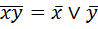 .
. в последнем случае ЭК пропадает).
в последнем случае ЭК пропадает). ).
).



