Многочлены Жегалкина
Мы уже заметили, что конъюнкция совпадает с обычным арифметическим умножением, попробуем ввести сложение: 0+0=0; 0+1-1; 1+0=1; 1+1=? Если принять 1+1=1, то получим дизъюнкцию. Если принять 1+1=0, то получим исключающее или. Принимаем второе соотношение: х+у=хÅу. Такое сложение совпадает с известным в теории чисел сложением по модулю 2. Заметим, что всегда хÅх=0. Всякая композиция сложений, умножений и констант называется арифметическим многочленом. Многочленом Жегалкина называют многочлен вида Теорема. Всякая булева функция может быть представлена в виде многочлена Жегалкина и притом единственным образом. Выразим три основные логические операции через сложение и умножение, превратив их в многочлены Жегалкина. Конъюнкция хÙу=ху уже готовый многочлен Жегалкина. Отрицание
|

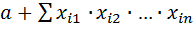 , где суммирование ведется по некоторому множеству различных наборов (i1, i2,…,ik), в котором ни один индекс не повторяется.
, где суммирование ведется по некоторому множеству различных наборов (i1, i2,…,ik), в котором ни один индекс не повторяется.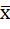 =хÅ1. Дизъюнкция
=хÅ1. Дизъюнкция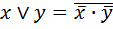 =(xÅ1)(yÅ1)+1= xy Å x Å y Å1Å1= xy Å x Å y.
=(xÅ1)(yÅ1)+1= xy Å x Å y Å1Å1= xy Å x Å y.


