ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Задача 1. a(0,1,1,0,1); b(0,1,1,1,1); a£b (a предшествует b).
Задача 1. a(0,1,1,0,1); b(0,1,1,1,1); a£b (a предшествует b). a(1,0,1,0,1); b(0,1,1,0,1); Решение. Наборы несравнимы, так как 1>0, 0<1.
Задача 2. Проверить функцию f(x,y)=x(x®y)«
Решение. (0;0)£(1;1) f(0;0)³f(1;1); (0;0)£(1;0) f(0;0)³f(1;0); (0;0)£(0;1) f(0;0)³f(0;1); (0;1)£(1;1) f(0;1)³f(1;1); (1;0)£(1;1) f(1;0)³f(1;1). Так как на меньшем наборе функция принимает большее значение, то в данном случае функция не является монотонной.
Теорема (критерий монотонности) Всякая дизъюнктивная нормальная форма (ДНФ), не содержащая отрицаний переменных, является монотонной функцией, отличной от констант 0 и 1. И наоборот: для любой монотонной функции, отличной от 0 и 1, существует равная ей ДНФ, не содержащая отрицаний переменных. 1. Двойственность. Двойственной функцией к булевой функции f(x 1, …, x n) называется функция f*=f ( 2. Самодвойственность S. БФ называется самодвойственной, если ее двойственная функция совпадает с самой функцией f, то есть f*=f.
|


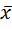
 ).
).


