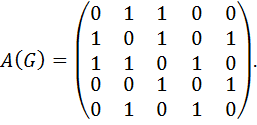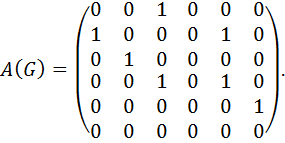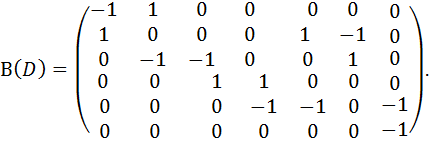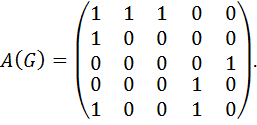ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Задача 1. Для графа G перечислить все вершины и ребра, указать степени всех вершин

Задача 1. Для графа G перечислить все вершины и ребра, указать степени всех вершин. Какие из них являются висячими, а какие изолированными?

v 5

v 6

v 4

v 3

v 2

v 1

x 6

x 5

x 3

x 4

x 2

x 1

3 bnJldi54bWxMj81OwzAQhO9IvIO1SFwq6tRSkxCyqVAlLnAACg/gxEsS4Z8Qu6n79rgnOI5mNPNN vYtGs4VmPzqLsFlnwMh2To22R/j8eLorgfkgrZLaWUI4k4ddc31Vy0q5k32n5RB6lkqsryTCEMJU ce67gYz0azeRTd6Xm40MSc49V7M8pXKjuciynBs52rQwyIn2A3Xfh6NBeH59W51FzFc/xbbdx6XU 8cVrxNub+PgALFAMf2G44Cd0aBJT645WeaYRtkWekghCFMAuvijStxbhflMCb2r+/0DzCwAA//8D AFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9U eXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9y ZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAAFOUeT1AQAA6wMAAA4AAAAAAAAAAAAAAAAALgIAAGRy cy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAK8SuWHdAAAACAEAAA8AAAAAAAAAAAAAAAAATwQA AGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAABZBQAAAAA= " strokecolor="black [3040]"/>

 

Решение. v ₁, v ₂, v ₃, v ₄, v ₅, v ₆, v ₇ – вершины графа G; ребра графа G – х ₁, х ₂, х ₃, х ₄, х ₅. Вершина v ₁ имеет степень 1, так как ей инцидентно только одно ребро х ₁. Вершина v ₂ имеет степень 4, так как ей инцидентны ребра х ₁, х ₂, х ₄, х ₅. Вершина v ₃ имеет степень 2, так как ей инцидентны два ребра х ₂ и х ₃ и т.д. Вершина v ₇ имеет степень 0, так как нет ребер ей инцидентных. Таким образом, вершины v ₁ и v ₆ являются висячими, так как их степень равна 1. Вершина v ₇ является изолированной, так как она имеет степень 0.

Задача 2. Для графа G построить матрицу смежности А(G).

v 5

v 4

v 3

v 2

v 1

x 6

x 5

x 3

x 4

x 2

x 1

 

Решение. Так как у графа 5 вершин, то размер матрицы А(G) будет 5х5. Так как вершины v ₁и v ₂ связаны ребром х ₁, то а ₁₂=1, так как вершины v ₁ и v ₃ связаны ребром х ₂, то а ₁₃=1, и т.д. В результате получаем матрицу смежности А(G):

 

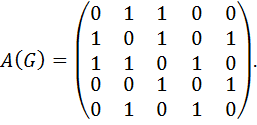
Заметим, что матрица смежности А(G) обладает свойством симметрии.

Задача 3. Пусть дан орграф D. Записать для графа D матрицу смежности А(D) и матрицу инцидентности В(D).

x 6

x 7

v 6

v 2

v 5

v 4

v 3

v 1

x 5

x 3

x 4

x 2

x 1

 

Решение. Орграф D содержит 6 вершин и 7 дуг, поэтому размер матрицы А(D) будет 6х6, а матрица В(D) – 6х7. Так как орграф D не содержит дуги из v ₁ в v ₁ (петли), то а ₁₁=0. Так как орграф D не содержит дуги из v ₁ в v ₂, то а ₁₂=0. Так как из вершины v ₁ в вершину v ₃ существует дуга х ₂, то а ₁₃=1 и т.д.

В результате получаем матрицу инцидентности А(D):

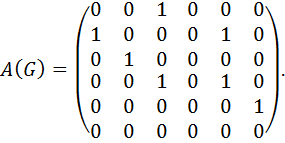
Матрица смежности А(D) орграфа D не обладает свойством симметрии.

Составим матрицу инцидентности В(D) орграфа D. Элемент b ₁₁=-1, так как в вершине v ₁ заканчивается дуга х ₁;

элемент b ₁₂=1, так как в вершине v ₁ заканчивается дуга х ₂ и т.д. В результате получаем матрицу инцидентности В(D):

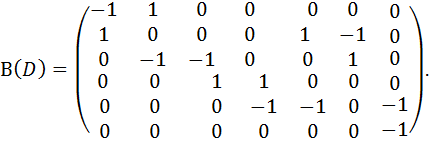
Задача 4. Пусть дан граф G. Определить количество путей длины 3 из вершины v ₂ в вершину v ₅.

x 78

v 2

x 6

x 7

v 5

v 4

v 3

v 1

x 5

x 3

x 4

x 2

x 1

 

 

Решение. Составим матрицу смежности графа G. Так как вершин у графа G равно 5, то матрица смежности имеет размерность 5х5.

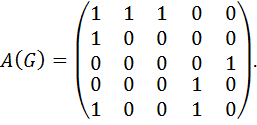
Так как необходимо определить пути длины 3, то матрицу смежности возведем в 3-ю степень.

Так как элемент а ₂₅=1, то из вершины v ₂ в вершину v ₅ существует один путь длины 3, а именно х ₂ х ₄ х ₆.