ПРИМЕР РЕШЕНИЯ ЗАДАЧ
Задача 1. Бросают две игральные кости. Сколькими способами они могут выпасть так, что на каждой кости выпадет четное число очков либо на каждой кости выпадет нечетное число очков? Решение. Пусть m – число возможностей для выпадения четного числа на одной кости, n – число возможностей для выпадения нечетного числа. Здесь m=n=3. По правилу произведения количество выпадения четных чисел, как и нечетных, равно 9. По правилу суммы количество возможностей для выпадения двух четных и двух нечетных чисел будет 18.
Задача 2. Сколько существует способов, чтобы расположить на полке 10 различных книг? Решение. При выборе 10 различных книг для расположения на полке важен порядок, то есть речь идет о перестановках без повторений, следовательно, используем формулу Pn=n! n=10 Þ P10=10!=10×9×8×7×6×5×4×3×2×1=3628800.
Задача 3. Группа из 15 человек выиграла 3 различные книги. Сколькими способами можно распределить эти книги среди группы? Решение. Выиграны три различные книги и при их распределении среди участников группы важен порядок. Это размещение без повторений, используем формулу
Задача 4. Группа из 15 человек выиграла 3 одинаковые книги. Сколькими способами можно распределить эти книги? Решение. При распределении книг (они одинаковые) между участниками группы порядок не важен. Мы имеем дело с сочетаниями без повторений. Используем формулу
Задача 5. Сколько различных слов можно получить, переставляя буквы в слове «м а т е м а т и к а»? Решение. Имеется 10 букв: букв «м» - 2, «а» - 3, «т» - 2, «е» - 1, «к» - 1. Итак, имеют место перестановки с повторениями, следовательно, используем формулу
Задача 6. Сколько пятизначных чисел можно составить, используя цифры: 1) 3,5,7,9; 2) 0;1;2. Решение. 1. Все пятизначные числа, составленные из цифр 3,5,7,9, отличаются друг от друга либо порядком их следования (35579 и 53579), либо самими цифрами (35795 и 57733). Следовательно, они являются размещениями из 4 элементов по 5 с повторениями, т.е. 2. Если пятизначные числа состоят из цифр 0,1,2, то первую цифру слева можно выбрать либо 1, либо 3 (0 не может занимать первую позицию). Таким образом, таких чисел будет
Задача 7. На почте пять видов открыток к Новому году. Сколькими способами из них можно выбрать семь открыток? Решение. Рассматриваемое множество состоит из 5 различных элементов, а выборки имеют объем, равный 7. Поскольку порядок выбора открыток к Новому году не играет роли, то искомое число возможностей составит набор поздравительных открыток к Новому году равно числу сочетаний с повторениями:
|

 , n=15, k=3. Итак,
, n=15, k=3. Итак, 
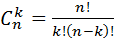 n=15, k=3. Итак,
n=15, k=3. Итак, 
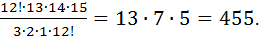
 для подсчета количества слов, составленных из букв слова «м а т е м а т и к а». n=10, k1=2, k2=3, k3=2, k4=1, k5=1, k6=1,
для подсчета количества слов, составленных из букв слова «м а т е м а т и к а». n=10, k1=2, k2=3, k3=2, k4=1, k5=1, k6=1,  .
. . Итак, искомое число пятизначных чисел равно
. Итак, искомое число пятизначных чисел равно  =1024.
=1024.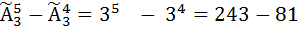 =162.
=162.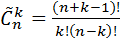 n=5, k=7.
n=5, k=7.  =330.
=330.


