Основные положения теории пограничного слоя
Поскольку основным предметом нашего рассмотрения должно явиться взаимодействие свободно или вынужденного движущегося потока жидкости или газа с поверхностью твердого тела необходимо вспомнить основные положения теории пограничного слоя [7]. Теплоотдача твердому телу зависит от распределения температуры в потоке жидкости или газа. Температурное поле в свою очередь зависит от гидродинамической обстановки в потоке жидкости, которая сложилась к заданному моменту времени. Следовательно, для решения тепловой задачи вначале необходимо найти распределения скоростей, т. е. решить гидродинамическую задачу. Если считать жидкость несжимаемой, (r = const), а теплоемкость постоянной (с = const), то в математическую формулировку гидродинамической задачи войдет уравнение неразрывности:
система уравнений движения Навье-Стокса
где X, Y, Z – проекции на оси координат внешних сил, действующих на элемент объема жидкости; Р – давление внутри жидкости; m – коэффициент динамической вязкости; v – скорость элемента объема жидкости. и уравнения, описывающие граничные условия 1, 2, 3 или 4-го рода. Главная трудность возникает при решении уравнений Навье-Стокса, которые представляют собой нелинейные дифференциальные уравнения в частных производных второго порядка. Кроме того, три уравнениясодержат четыре неизвестных – vх, vу, vz,P. Только при больших упрощениях, эти уравнения удалось решить. Например, при натекании жидкости из бесконечности на бесконечную стенку. Известны приближенные решения уравнений Навье-Стокса для так называемого ползущего движения, первого предельного случая, очень малой скорости. Но наибольший интерес представляет второй предельный случай – очень малой вязкости жидкости при большой скорости. Метод упрощения дифференциальных уравнений Навье-Стокса для второго предельного случая был разработан Прандтлем. В 1904 г он представил по этому поводу доклад Международному конгрессу математиков в Гейдельберге. Сущность метода поясним на примере стационарного плоскопараллельного потока жидкости, омывающего пластину. Поток жидкости, омывающий тело, мысленно разбивают на две области: пограничный слой 1 и внешний поток 2.
Гидродинамическим (динамическим) пограничным слоем называют область течения вязкой теплопроводной жидкости, характеризующейся малой толщиной d(х) по сравнению с продольными размерами области (например, длиной пластины ℓ, d(х) << ℓ;) и большим поперечным градиентом, скорости  .Скорость жидкости vx у стенки равна нулю (эффект прилипания). Переход vx к V¥ осуществляется асимптотически. Однако практически величина vx достигает значения v, близкого к V¥ (v1 = 0,99 V¥) в очень тонком слое, толщина которого обычно принимается за толщину пограничного слоя d(х). .Скорость жидкости vx у стенки равна нулю (эффект прилипания). Переход vx к V¥ осуществляется асимптотически. Однако практически величина vx достигает значения v, близкого к V¥ (v1 = 0,99 V¥) в очень тонком слое, толщина которого обычно принимается за толщину пограничного слоя d(х).
То есть, для гидродинамического пограничного слоя удается значительно упростить уравнения Навье-Стокса. Полученные после упрощения уравнения называют уравнениями динамического пограничного слоя. Для внешнего потока уравнения Навье-Стокса так же упрощаются (последнее слагаемое с m пропадает, т. к. силами внутреннего трения в жидкости пренебрегают). Итак, исследуемый поток разбивается на две части и задача математического описания течения жидкости при этом упрощается. Наряду с динамическим пограничным слоем существует также и тепловой пограничный слой. Он характеризуется большим поперечным градиентом температуры, под действием которого осуществляется поперечный перенос теплоты. Распределение температур внутри движущейся несжимаемой жидкости в случае нестационарного трехмерного температурного поля описывается дифференциальным уравнением
Для теплового пограничного слоя удается упростить это уравнение. Полученное после упрощения уравнение называют уравнением энергии теплового пограничного слоя. Можно получить точное аналитическое решение (распределение температуры в пограничном слое) этого уравнения, если из гидродинамической задачи определено распределение скорости пограничного слоя. Точные решения уравнений динамического и теплового пограничного слоев трудоемки, а в ряде случаев и не возможны, потому в инженерных расчетах часто пользуются приближенными методами решения указанных уравнений (метод теории подобия – см. п. 3.5.4 – 3.5.8). Таким образом, сущность теории пограничного слоя состоит в упрощении уравнений, описывающих процесс теплообмена между твердым телом и омывающей его жидкостью на основании применения их к малой пространственной области – пограничному слою и отыскания методов решения полученных после упрощения уравнений. Для решения задачи теплоотдачи от жидкости или газа к твердому телу рассмотренные уравнения осталось дополнить граничными условиями. Чаще всего используют граничные условия третьего рода (см. п 3.3.4):
где l0 – коэффициент теплопроводности среды; у – ось системы координат с началом на поверхности теплообмена, направленная внутрь жидкости и твердого тела; tS, t0 – собственно температура поверхности и среды; a – коэффициент теплоотдачи.
|

 , (5.1)
, (5.1) , (5.2)
, (5.2) – полная или субстанциональная производная (оценивает действительное ускорение, которое испытывает частица, проходя вдоль линии тока в поле скорости);
– полная или субстанциональная производная (оценивает действительное ускорение, которое испытывает частица, проходя вдоль линии тока в поле скорости);
 . (5.3)
. (5.3)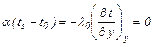 , (5.4)
, (5.4)


