Интегральный переход третьего типа
Для того, чтобы получить формулу, описывающую процесс распространения теплоты от движущегося источника, необходимо выполнить третий интегральный переход. По сути, он является разновидностью второго. Следует лишь учесть, что расстояние R для движущегося источника является переменной величиной. Например, если источник движется вдоль оси Х со скоростью v, то:
Рассмотрим одномерный источник J1 c равномерно распределенной мощностью тепловыделения q1, Вт/м (рис. 4.3), движущийся из т. О1 по направлению стрелки со скоростью v, м/с. Источник попадает последовательно в положения 1, 2,.., i,.., каждый раз внося в тело элементарную порцию теплоты dQ1 на единице длины. Каждый из таких импульсов, например, i -й, можем рассматривать как мгновенный одномерный источник вспыхнувший и погасший на расстоянии Ri от точки М(х, у). Этот импульс в соответствии с формулой (4.11) вызовет в точке М элементарное повышение температуры:
так как уu = 0 (источник лежит в плоскости XOZ). Свяжем систему координат с движущимся источником. Пусть в момент наблюдения t система с источником находится в точке О. Тогда время распространения теплоты импульса θi равно t - θi, а абсцисса этого импульса xu = v (t -θi).
Рис. 4.3. Движущийся одномерный J1 и двумерный (полосовой) J2 источники теплоты
Далее заметим, что dQ1 = q1×dθi и:
Все импульсы, которыми имитируется движение источника, дадут в точке М(x, y) общее повышение температуры:
Эта формула описывает температурное поле в тепловой задаче В этом случае, полагая:
преобразуем выражение для расчета t(x,y,z) к виду:
поскольку:
где К0 [ u ] – модифицированная функция Бесселя от мнимого аргумента второго рода, нулевого порядка. С погрешностью, не выходящей за пределы 5 % можно полагать, что:
причем m = 0,342 + 0,053u при 0 ≤ u ≤ 3 и m = 0,5 при u > 3. От выражения (4.24) можем перейти к формуле для описания температурного поля в задаче
Используем далее безразмерные координаты:
где ℓ; - длина источника в направлении движения. Если
где:
Значения Т(y,v) при конкретных значениях Рe, y, v определяют каким либо из способов приближенного вычисления интегралов. Для решения вопроса о температуре точек тела, лежащих в плоскости ХО1Z (ν = 0) можно в качестве первого приближения воспользоваться выражением для К0[u]. Например, наибольшее значение функции Т(y, v) = Т(1, 0) = Тmax можем получить положив u = 0,5Рe(y - yu) и приняв некоторое среднее значение показателя m в формуле для K0[u]. Интегрирование в этом случае дает следующее выражение:
|

 , (4.19)
, (4.19) . (4.20)
. (4.20)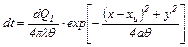 , (4.21)
, (4.21)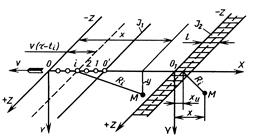
 (4.22)
(4.22) (4.23)
(4.23) . Интеграл в этом выражении приводится к изученным функциям только при t ® ¥, т. е. для задачи, код которой
. Интеграл в этом выражении приводится к изученным функциям только при t ® ¥, т. е. для задачи, код которой  .
. и
и 
 , (4.24)
, (4.24) , (4.25)
, (4.25)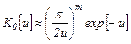 , (4.26)
, (4.26) для полосового источника, движущегося с любой скоростью по оси О1Х. Если какой-либо из одномерных источников, образующих полосовой, имеет абсциссу Xu, то расстояние от него до точки М(х, у) тела равно
для полосового источника, движущегося с любой скоростью по оси О1Х. Если какой-либо из одномерных источников, образующих полосовой, имеет абсциссу Xu, то расстояние от него до точки М(х, у) тела равно 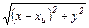 . Поэтому переходя от одномерного источника к полосовому с равномерным тепловыделением q2, запишем:
. Поэтому переходя от одномерного источника к полосовому с равномерным тепловыделением q2, запишем: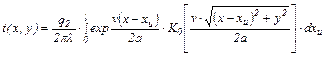 (4.27)
(4.27) ,
, , то получим:
, то получим: , (4.28)
, (4.28) . (4.29)
. (4.29) . (4.30)
. (4.30)


