Быстродвижущиеся источники
Методику получения формул для быстродвижущихся источников теплоты покажем на примере тепловой задачи Для такой задачи мы уже получили уравнение (4.12) при осуществлении первого интегрального перехода. Чтобы применить эту формулу к данному случаю, отметим, что yu = 0, а время, прошедшее с того момента, когда источник «проскочил» элемент dx, до момента наблюдения
Возвратимся к полосовому источнику J2 и предположим, что он быстродвижущийся. Тогда для этого источника:
Верхний предел интегрирования р зависит от абсциссы х точки, для которой рассчитывается температура. Если x ³ l, то р = l, т. к. на температуру точки М влияют все одномерные источники, образующие плоский. Если же x < l, то р = х, т. к. теплота, выделяемая быстродвижущимся источником, впереди источника не распространяется. Используя безразмерные координаты ψ, ψu, ν, получим
или:
где:
Верхний предел интеграла D = y при 0 £ y £ 1 и D = 1 при y > 1. Для точек, лежащих в плоскости движения источника (n = 0), выполняя интегрирование, получаем: при 0 ≤ ψ ≤ 1, при ψ > 1, Относительная температура Т1 (y, n) при y = 1 и n = 0 имеет наибольшее значение Т1max = 1. До сих пор мы рассматривали источники, тепловыделение которых равномерно распределено по пятну нагрева. Если теплота распределена на пятне нагрева по какому-либо другому закону, то методика интегральных переходов остается прежней, но под соответствующие интегралы дополнительно вводится функция, описывающая закон распределения плотности тепловых потоков. Например, если тепловыделение быстродвижущегося полосового источника описывается формулой q2(y) = q0 f(yu), то вместо выражения (4.35) получаем:
Соответственно видоизменяется и функция Т1(y, n), значения которой приходится определять методами приближенного интегрирования.
|


 . Пусть одномерный источник J1 с равномерно распределенной плотностью тепловыделения q1 движется с высокой скоростью v в направлении, показанном стрелкой на рисунке. Система координат XYZ движется вместе с источником. Выделим из неограниченного тела элемент в виде стержня шириной b и толщиной dx. Вследствие высокой скорости движения время «проскакивания» источника через этот элемент
. Пусть одномерный источник J1 с равномерно распределенной плотностью тепловыделения q1 движется с высокой скоростью v в направлении, показанном стрелкой на рисунке. Система координат XYZ движется вместе с источником. Выделим из неограниченного тела элемент в виде стержня шириной b и толщиной dx. Вследствие высокой скорости движения время «проскакивания» источника через этот элемент  столь мало, что на участке b∙dx температуру можно считать одинаковой во всех точках, а сам источник в этом элементе полагать двумерным мгновенным.
столь мало, что на участке b∙dx температуру можно считать одинаковой во всех точках, а сам источник в этом элементе полагать двумерным мгновенным. . Что касается тепловыделения Q2 двумерного источника, то оно связанно с плотностью q1 тепловыделения одномерного источника уравнением теплового баланса для площадки b∙dx, а именно b∙q1dt = bQ2dx откуда
. Что касается тепловыделения Q2 двумерного источника, то оно связанно с плотностью q1 тепловыделения одномерного источника уравнением теплового баланса для площадки b∙dx, а именно b∙q1dt = bQ2dx откуда 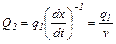 . Подставляя эти преобразования в формулу (4.12), получим для быстродвижущегося одномерного источника:
. Подставляя эти преобразования в формулу (4.12), получим для быстродвижущегося одномерного источника: . (4.31)
. (4.31)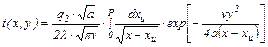 . (4.32)
. (4.32)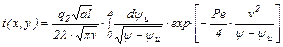 . (4.33)
. (4.33) , (4.34)
, (4.34)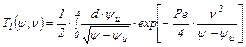 . (4.35)
. (4.35)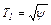 ; (4.36)
; (4.36)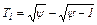 . (4.37)
. (4.37) . (4.38)
. (4.38)


