Пример 6.31.
В схеме на рис. 6.13 параметры цепи такие: напряжение 220 В, сопротивления r = 10 Ом, r2 = 50 Ом, r3 = 5 Ом. Найти общий ток Решение 1. ток в резисторе r1 I1 = 2. ток в резисторе r2 I2 =
3. ток в резисторе r3 I3 = 4. общий ток I = I1 + I2 + I 3 = 22 + 4,4 + 44 = 70,4 А.
При большом числе параллельно включенных приемников расчет общего тока, приведенный в примере 1.22, становится громоздким и требует много времени, т. к. приходится рассчитывать ток по отдельности для каждого приемника. Поэтому при расчете таких цепей гораздо удобней использовать метод эквивалентной проводимости цепи. Суть метода состоит в том, что для каждой ветви рассчитывают её проводимость, после чего находят эквивалентную проводимость всей цепи как сумму проводимостей ветвей, а уже по ней – общий ток (см. пример 1.23). Таким образом, отпадает необходимость рассчитывать по отдельности токи каждой параллельной ветви. Опуская математические выкладки, приведем «готовые» соотношения для расчёта эквивалентного сопротивления цепи с параллельным соединением нескольких резисторов. Эквивалентное сопротивление цепи rэ = где В свою очередь, gэ = g где g Теперь можно выразить закон Ома для участка цепи через эквивалетную проводимость I =
|
=
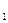= 22 А
= 4,4 А
= 44 А
, (6.44)
- эквивалентная проводимость цепи.
+ …+ g 
, (6.45)
Ugэ. (6.46)
