Пример 6.40.
В схеме на рис. 6.15, а для каждого резистора рассчитать ток в нем и падение напряжения на нем, а также составить баланс мощностей. Исходные данные – в примере 6.38. Расчет Начало расчета повторяет расчет, приведенный в пп. 1, 2 и 3 примера 6.38: 1. эквивалентное сопротивление резисторов r2 и r3 : 2. эквивалентное сопротивление всех трех резисторов
3. ток цепи
Это ток протекает в неразветвленной части цепи, т.е. через резистор а в точке В делится на токи Значит, ток в этом резисторе Далее расчет продолжается следующим образом: 4. падение напряжения на резисторе
5. чтобы найти токи в резисторах r2 и r3, сначала найдем падение напряжение на этих резисторах (напряжение между точками В и С)
6. по закону Ома, ток в каждом резисторе
7. для проверки правильности расчета используем 1-й и 2-й закон Кирхгофа. По 1-му закону Кирхгофа, для точки В справедливо уравнение
По 2-му закону Кирхгофа, напряжение сети равно сумме напряжений между точками А, В и В, С, т.е.
Поскольку обе проверки в числах правильны, задача решена верно. 8. баланс мощности цепи состоит в том, мощность источника питания цепи должна равняться сумме мощностей всех приемников электроэнергии. В данном примере мощность источника цепи
а мощности приемников равны соответственно
В общем виде уравнение баланса мощностей такое
Поскольку проверка в числах правильна, задача решена верно. 9. при расчете баланса мощности, кроме формулы 1.17, можно также использовать формулы 1.18 и 1.20, на основании которых
10. Поскольку полученные в этом пункте результаты расчета совпадают с результатами п. 8, баланс мощностей можно не составлять.
|

 =
=  = 24 Ом
= 24 Ом = 20 + 24 = 44 Ом
= 20 + 24 = 44 Ом =
=  5 А.
5 А.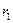 (рис. 1.8, а),
(рис. 1.8, а), и
и  .
. = 5 А.
= 5 А.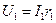 = 5*20 = 100 В
= 5*20 = 100 В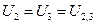 =
=  := 5*24 = 120 В.
:= 5*24 = 120 В. = 3 А,
= 3 А, = 2 А.
= 2 А. , или, в числах 5 = 3 +2 (А).
, или, в числах 5 = 3 +2 (А). , или в числах 220 = 100 + 120 (В).
, или в числах 220 = 100 + 120 (В). Вт,
Вт, Вт,
Вт, = 120*3 = 360 Вт,
= 120*3 = 360 Вт, 240 Вт.
240 Вт.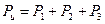 , или в числах 1100 = 500 + 360 + 240 (Вт).
, или в числах 1100 = 500 + 360 + 240 (Вт). Вт или
Вт или 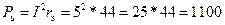 Вт
Вт Вт или
Вт или  = 52 *20 = 25*20 = 500 Вт,
= 52 *20 = 25*20 = 500 Вт, =
= 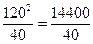 = 360 Вт или
= 360 Вт или  360 Вт
360 Вт = 240 Вт или
= 240 Вт или  = 22*60 = 240 Вт.
= 22*60 = 240 Вт.


