Графическое изображение синусоидальных величин
Для изображения синусоидальных величин используют два вида графиков (диаграмм): 1. волновые; 2. векторные.
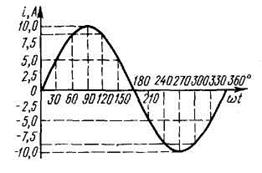
Рис. 6.52. Волновая диаграмма синусоидального тока Волновые диаграммы очень наглядны (рис. 6.52), но для их построения надо предварительно рассчитать множество значений синусоидальной величины для разных моментов времени (разных углов поворота рамки). Например, для построения графика на рис. 6.52 надо рассчитать значения тока для 13 значений углов поворота рамки: 0º, 30º, 60º, …. 360º. Однако на практике гораздо чаще применяются векторные диаграммы. Они не требуют утомительных расчетов, просты и достаточно наглядны. Векторной называется диаграмма, на которой одна или несколько синусоидальных величин изображены в виде неподвижных векторов. Для того, чтобы синусоидальную величину изобразить в виде вектора, необходимо записать закон изменения, например,
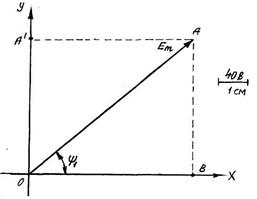
Рис. 6.53. Графическое (в виде вектора) изображение синусоидальной ЭДС, которая изменяется по закону
После этого: 1. в прямоугольной системе координат отложить угол, равный начальной фазе, в данном примере, угол ψ = 45º (рис. 6.53). При этом углы откладываются относительно положительной полуоси таким образом: если угол положительный – в направлении против часовой стрелки, если угол отрицательный – по часовой. В данном случае угол ψ = 45º отложен относительно положительной полуоси в направлении против часовой стрелки. 2. выбирают масштаб, удобный для построения вектора (чтобы вектор поместился на диаграмме), после чего в этом масштабе откладывают под построенным углом отрезок, равный максимальному (амплитудному) значению синусоидальной величины. В данном примере, максимальное значение ЭДС Таким образом, на диаграмме длина вектора 3. конец вектора обозначают стрелкой, направленной от начала координат. Как следует из приведенного выше объяснения, вектор представляет собой синусоидальную величину, значение которой, т.е. длина вектора, соответствуют начальному моменту времени, т.е. Мгновенное значение синусоидальной величины равно проекции вектора на вертикальную ось, в нашем примере – отрезку АВ. Действительно, из прямоугольного треугольника ОАВ длина вертикального катета АВ = Такое же мгновенное значение ЭДС получается, если в закон её изменения подставить время
Внимание! На векторной диаграмме изображаются синусоидальные величины, имеющие одинаковую частоту.
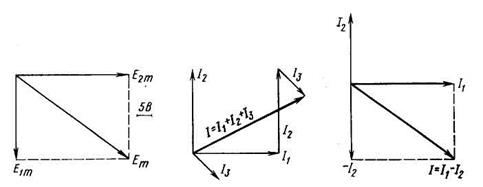
Действия над векторами Чаще всего векторы приходится складывать или вычитать. Если векторов – только два, то для этого используют известное из курса тригонометрии правило параллелограмма. Это правило состоит в следующем: из конца первого вектора проводят вспомогательную прямую, параллельную второму вектору, а затем – наоборот. Чтобы получить суммарный вектор, точку пересечения этих прямых соединяют с началом координат (рис. 6.54, а).
Рис. 6.54: Сложение двух токов (а); сложение трёх токов (б); вычитание токов (в)
Если нужно сложить не два, а большее число векторов, удобно использовать правило многоугольника: векторы переносятся параллельно самим себе так, чтоб начало второго вектора совпадало с концом первого, начало третьего – с концом второго и т.д. (рис. 6.54, б). Для того, чтобы из одного вектора вычесть другой, необходимо к первому вектору добавить второй, но взятый с обратным знаком. Для этого второй вектор надо повернуть на 180º, по или против часовой стрелки – без разницы (рис. 6.54, в).
|

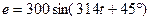 .
.
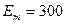 В, выбираем удобный масштаб
В, выбираем удобный масштаб 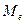 = 20 В/см.
= 20 В/см.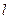 = 300/20 = 15 cм (ширина листа формата А4 – 198 мм, т.е. вектор поместится на диаграмме, если даже расположить его горизонтально).
= 300/20 = 15 cм (ширина листа формата А4 – 198 мм, т.е. вектор поместится на диаграмме, если даже расположить его горизонтально).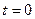 .
.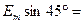 300*0,707 = 212,1 В.
300*0,707 = 212,1 В.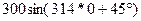 =
= 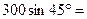 300*0,707 = 212,1 В.
300*0,707 = 212,1 В.